높거나 낮은 지점에서 함수는 어디에 있습니까? 미적분이 도움이 될 수 있습니다!
최대 값은 높은 점이고 최소 값은 낮은 점입니다:
부드럽게 변화하는 함수에서 최대 또는 최소는 항상 함수가 평평 해지는 곳입니다(중철 점 제외).
어디에서 평평하게합니까? 여기서 기울기는 0 입니다.
기울기 0 은 어디에 있습니까? 파생 상품은 우리에게 알려줍니다!
예를 들어 보자:
예:공이 공중에 던져집니다. 그것의 높이 언제 든 지 티에 의해 주어진다:
시간=3+14 톤−5 톤 2
최대 높이 무엇입니까?
미분을 사용하여 해당 함수의 기울기를 찾을 수 있습니다:
3352 0 + 14 − 5(2 티)
=14−10 티
(우리가 그 미분을 발견 한 방법에 대한이 예 아래를 참조하십시오.)
이제 기울기가 0 일 때 찾습니다.
기울기는 티=1.4 초
에서 0 이고 그 때의 높이는:
이 경우 최대 높이는 12.8 미터(티=1.4 초)입니다.)
파생 상품
에 대한 빠른 재교육 파생 상품은 기본적으로 함수의 기울기를 찾습니다.
이전 예에서 우리는 이것을 취했다:
시간=3+14 티−5 티 2
이 미분을 내놓았다:
0 + 14 − 5(2 티)
=14−10 티
언제든지 함수의 기울기를 알려줍니다 티
우리는 이러한 파생 규칙을 사용했습니다:
- 상수 값의 기울기(예:3)는 0
- 2 와 같은 선의 기울기는 2 입니다.: 0 + 14 − 5(2 톤)
그것이 최대(또는 최소)인지 어떻게 알 수 있습니까?
우리는 그래프에서 그것을 보았다! 그러나 그렇지 않습니다… 파생 상품은 다시 구조에 온다.
이것은 기울기가 계속 작아지고 있음을 의미합니다(-10):왼쪽에서 오른쪽으로 이동하면 기울기가 양수로 시작되고(함수가 상승)0(평점)을 통과 한 다음 기울기가 음수가됩니다(함수가 떨어집니다):
기울기가 작아지고(0 이 되더라도)최대 값을 의미합니다.
이것은 제 2 미분 검정
위의 그래프에서 전후의 기울기를 보여 주었지만 실제로는 기울기가 0 인 지점에서 테스트를 수행합니다:
두 번째 파생 테스트
함수의 기울기가 0 인 경우 엑스,그리고 두 번째 미분 엑스:
- 0 보다 작 으면 로컬 최대
- 0 보다 크며 로컬 최소
- 0 과 같으면 테스트가 실패합니다(다른 방법으로 찾을 수 있지만)
“2 차 도함수:0 보다 작으면 최대값이고 0 보다 크면 최소값입니다”
예:최대 값과 최소값을 찾습니다.
와이=5 엑스 3+2 엑스 2−3 엑스
미분(기울기)은:
6347− 3
0 이 있는 2 차입니다:
- 엑스= -3/5
- 엑스= +1/3
그들은 최대 또는 최소 될 수 있을까? (아직 그래프를 보지 마세요!2830>
2 차 미분값은 다음과 같습니다.”=30 배+4
= -3/5:
입니다.= +1/3:
입니다(이제 그래프를 볼 수 있습니다.)
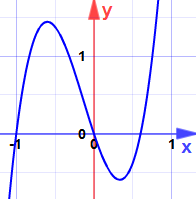
단어
높은 점을 최대(복수 최대)라고합니다.
낮은 점을 최소(복수 최소)라고합니다.
최대 또는 최소의 일반적인 단어는 극단(복수 극단)입니다.
우리는 다른 곳에서 더 높은(또는 더 낮은)점이있을 수 있지만 근처에 없을 때 지역 최대(또는 최소)라고 말합니다.2830>
또 하나의 예
예:최대값과 최소값 찾기:
와이=엑스 3−6 엑스 2+12 엑스−5
미분값은:
+ 12
는 최대 또는 최소입니까?1946 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년 12 월 2830 년” = 6(2) − 12 = 0
테스트가 실패하고 그 이유는 다음과 같습니다:
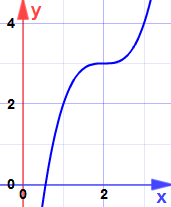
그것은 안장 포인트입니다… 기울기는 0 이 되지만 최대값이나 최소값은 아닙니다.
은
을 구분할 수 있어야 하며 중요한 기술적 요점이 있습니다:
함수는 미분 가능해야 합니다(미분은 해당 도메인의 각 지점에 존재해야 함). 예:함수 에프(엑스)=|엑스|(절대 값)?
| |엑스/다음과 같습니다: |  |
에서 엑스=0 그것은 매우 뾰족한 변화가 있습니다!
사실 그것은 차별화 할 수 없습니다(차별화 가능한 페이지에 표시됨).
그래서 우리는 절대 값 함수에이 방법을 사용할 수 없습니다.
함수도 연속적이어야 하지만 차별화 가능한 함수도 연속적이므로 걱정할 필요가 없습니다.




