hvis vårt mål er å finne den relativistiske generaliseringen Av Poisson ‘ s ligning for gravitasjonsfeltet:
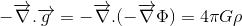
Der Φ refererer til gravitasjonspotensialet og ρ til massetettheten, er vi halvveis.
faktisk har vi allerede sett i vår forrige artikkel energi-momentum tensor at generaliseringen av massetettheten (høyre term av ligningen) tilsvarer energi-momentum Tµ.
det virker rimelig å anta at vår ligning skal ta form av:
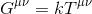
Hvor k står For en skalar Og Gµ, kalt Einstein tensor representerer en rang-2 tensor som beskriver spacetime krumning .
Så vidt Vi vet, Bør Gµ overholde følgende begrensninger:
– det bør oppheve i flat tidsrom
– det bør beskrive tidsrom krumning og være lineær med hensyn Til Riemann tensor
– det bør være symmetrisk og av rang 2 (Som Tµ)
– det bør ha en null divergens (Som Tµ)
– og til slutt, i newtonske grenser, det bør redusere til 4ngp
første forsøk med ricci tensor som løsning
vi husker fra Vår Artikkel den geodetiske ligningen i den newtonske grensen at gravitasjonspotensialet φ er knyttet til 00-komponenten Av Metriske Via H00=(g00-1)/c2
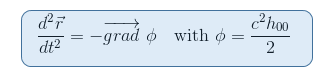
Det virker da naturlig å se etter en tensor som involverer de andre derivatene av metriske, som er tilfelle For Riemann tensor. Videre Er Riemann tensor den eneste kandidaten vi vet så langt for å kunne beskrive romtidskurvaturet (cf andre begrensning ovenfor).
som vi må finne en rang-2 tensor, og hvis vi antar at vi må finne en løsning utelukkende når Det Gjelder Riemann tensor, virker det naturlig å først vurdere den kontraherte formen Av Riemann tensor, kjent som Ricci tensor.
for å se dette, la oss huske uttrykket Av Riemann tensor fra artikkelen Riemann curvature tensor part II: derivasjon fra geodetisk avvik
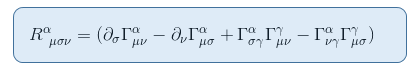
i grensen til et statisk og svakt gravitasjonsfelt bidrar bare ett begrep Til R00:
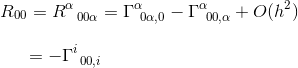
I samme artikkel har vi beregnet Dette Christoffel-symbolet og funnet ut at
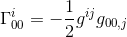
med tilnærmingen til gij = nij og goo,j = hoo, j (se artikkelen) får vi:
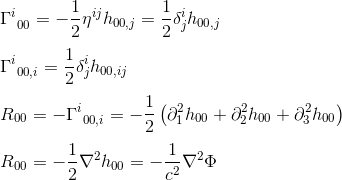
identifikasjonen Av R00 med ΔΦ (laplacian Operatør) antyder at feltligningen i generell relativitet skal likestille rab til et konstant multiplum av tab.
I 1915, ved hjelp av denne ligningen, Var Einstein selv i stand til å løse det langvarige problemet Med Kvikksølvperihelionpresesjon, noe som førte til å skrive i November det året at » i noen dager var jeg fra meg selv med glede.»
Til Slutt Måtte Einstein avvise dette første forsøket, på grunn av det faktum at Generelt divergens Av Rab ikke opphever.
Andre forsøk
det er tensor nært knyttet Til Ricci skalar wihch kan settes på venstre side uten motsigelse. Dette gir Einstein tensor definert som følger:
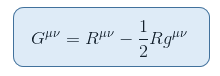
Hvor R = Raa Er Ricci skalar eller skalar kurvatur.
denne Formen for Gab er symmetrisk og av rang-2 og beskriver åpenbart spacetime-krumningen. Så det er bare å vise at totalderivatet er null
for å gjøre Dette starter Vi Med Bianchi-identiteten
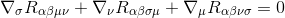
Multiplikasjon gjennom med gγσαμ (metrikkderivatene er null, slik at de fungerer som konstanter og kan tas inn i derivatene), gir det til:
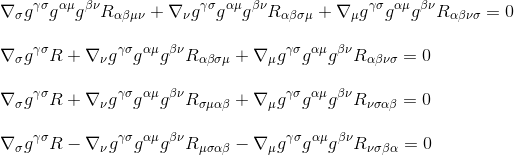
Ved å bruke Ricci-tensordefinisjonen Rµ=gμβνσ (trinn 3) og ved å gi indeksene et nytt navn (trinn 4), får vi
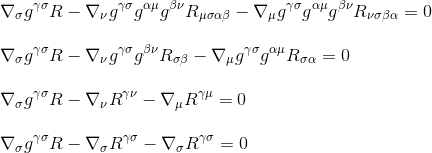
ved å faktorisere derivatet får vi endelig
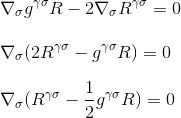
det er akkurat det vi ønsket å demonstrere: divergensen Av Einstein tensor er null, og vi har funnet den rette kandidaten til venstre side av vår krumning / masse-energi ligning.