Interkvartile Områder & Outliers

• Purplemath
• MathHelp.com
• Finn utligningene, hvis noen, for følgende datasett:
• Finn outliers og ekstreme verdier, hvis noen, for følgende datasett, og tegne box-and-whisker-plottet. Merk eventuelle uteliggere med en stjerne og eventuelle ekstreme verdier med en åpen prikk.

Purplemath

«interquartile range», forkortet «IQR», er bare bredden på boksen i box-and-whisker-plottet. DET vil SI, IQR = Q3-Q1 . IQR kan brukes som et mål på hvor spredt verdiene er.

Statistikk antar at verdiene dine er gruppert rundt en sentral verdi. IQR forteller hvordan spredt ut de» midtre » verdiene er; det kan også brukes til å fortelle når noen av de andre verdiene er «for langt» fra den sentrale verdien. Disse» for langt unna «punktene kalles «outliers», fordi de» ligger utenfor » området der vi forventer dem.

IQR er lengden på boksen i box-and-whisker-plottet. En outlier er en verdi som ligger mer enn en og en halv ganger lengden på boksen fra hver ende av boksen.

Innholdet Fortsetter Nedenfor

MathHelp.com

Det vil si at hvis et datapunkt er under Q1 – 1.5×IQR eller over Q3 + 1.5×iqr, anses det for å være for langt fra de sentrale verdiene til å være rimelige. Kanskje du bumped veieskalaen når du gjorde den ene måling, eller kanskje din laboratoriepartner er en idiot, og du burde aldri ha latt ham røre noe av utstyret. Hvem vet? Men uansett årsak, er outliers de punktene som ikke ser ut til å «passe».

Når du er komfortabel med å finne IQR, kan du gå videre til å finne uteliggere, hvis noen.

• Finn utligningene, hvis noen, for følgende datasett:

verdiene For Q1-1.5 hryvnias IQR og Q3 + 1.5 hryvnias IQR er «gjerder» som markerer de «rimelige» verdiene fra outlier-verdiene. Uteliggere ligger utenfor gjerdene.

hvis oppgaven din har, vurderer du ikke bare uteliggere, men også «ekstreme verdier», så verdiene For Q1 – 1.5 hryvnias IQR og Q3 + 1,5 hryvnias iqr er de «indre» gjerdene og verdiene For Q1-3 hryvnias IQR og Q3 + 3 hryvnias IQR er de «ytre» gjerdene.

uteliggerne (merket med stjerner eller åpne prikker) er mellom de indre og ytre gjerdene, og de ekstreme verdiene (merket med hvilket symbol du ikke brukte for utligningene) er utenfor de ytre gjerdene.

for øvrig kan boken din referere til verdien av » 1,5×IQR «som et»trinn». Da vil uteliggerne være tallene som er mellom ett og to trinn fra hengslene, og ekstremverdien vil være tallene som er mer enn to trinn fra hengslene.

ved å se på forrige eksempel igjen, vil de ytre gjerdene være på 14.4-3×0.5 = 12.9 og 14.9 + 3×0.5 = 16.4. Siden 16.4 er rett på det øvre ytre gjerdet, vil dette anses å være bare en outlier, ikke en ekstrem verdi. Men 10.2 er helt under det nedre ytre gjerdet, så 10.2 ville være en ekstrem verdi.

din grafisk kalkulator kan eller ikke kan indikere om en boks-og-whisker tomten inkluderer uteliggere. For eksempel inkluderer problemet ovenfor punktene 10.2, 15.9 og 16.4 som uteliggere. En innstilling på min grafisk kalkulator gir enkel box-and-whisker plot som bruker bare fem-nummer sammendrag, så lengst uteliggere vises som endepunktene på værhår:

en annen kalkulatorinnstilling gir boksen og whisker-plottet med utligningene spesielt merket (i dette tilfellet med en simulering av en åpen prikk), og vispene går bare så langt som de høyeste og laveste verdiene som ikke er utliggere:

kalkulatoren min skiller ikke mellom outliers og ekstreme verdier. Kanskje ikke din heller. Sjekk din brukerhåndbok nå, før neste test.

hvis du bruker grafisk kalkulator for å hjelpe til med disse tomter, sørg for at du vet hvilken innstilling du skal bruke og hva resultatene betyr, eller kalkulatoren kan gi deg en helt riktig, men «feil» svar.

• Finn outliers og ekstreme verdier, hvis noen, for følgende datasett, og tegne box-and-whisker-plottet. Merk eventuelle uteliggere med en stjerne og eventuelle ekstreme verdier med en åpen prikk.

Annonse

for å finne outliers og ekstreme verdier, må jeg først finne IQR. Siden det er syv verdier i listen, er medianen den fjerde verdien, så:

Q2 = 25

første halvdel av listen er:

21, 23, 24

…så Q1 = 23; den andre halvdelen er:

29, 33, 49

…så Q3 = 33. DA ER IQR gitt av:

IQR = 33 – 23 = 10

uteliggere vil være noen verdier under:

23 – 1.5×10 = 23 – 15 = 8

…eller over:

33 + 1.5×10 = 33 + 15 = 48

de ekstreme verdiene vil være de nedenfor:

23 – 3×10 = 23 – 30 = -7

…eller over:

33 + 3×10 = 33 + 30 = 63

Så jeg har en outlier på 49, men ingen ekstreme verdier. Jeg vil ikke ha en topp whisker på min tomt fordi Q3 er også den høyeste ikke-outlier. Så min tomt ser slik ut:

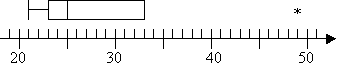
det skal bemerkes at metodene, vilkårene og reglene som er skissert ovenfor, er det jeg har lært og hva jeg oftest har sett lært. Kurset ditt kan imidlertid ha forskjellige spesifikke regler, eller kalkulatoren din kan gjøre beregninger litt annerledes. Du må kanskje være litt fleksibel for å finne svarene som er spesifikke for læreplanen din.