Område Treghetsmoment-Typiske Tverrsnitt I

Område Treghetsmoment eller Treghetsmoment for Et Område – også kjent som Andre Øyeblikk Av Område – I, er en egenskap av form som brukes til å forutsi avbøyning, bøyning og stress i bjelker.

Område Treghetsmoment – Britiske enheter

• inches4

Område Treghetsmoment – Metriske enheter

• cm4
• m4

konvertering mellom enheter

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4. 16×105 mm4 = 41.6 cm4

Eksempel – Konverter Mellom Arealmoment Av Treghet Enheter

9240 cm4 kan konverteres til mm4 ved å multiplisere med 104

(9240 cm4) 104 = 9.24 107 mm4

Treghetsmoment (Treghetsmoment for Et Område eller Andre Moment Av Området)

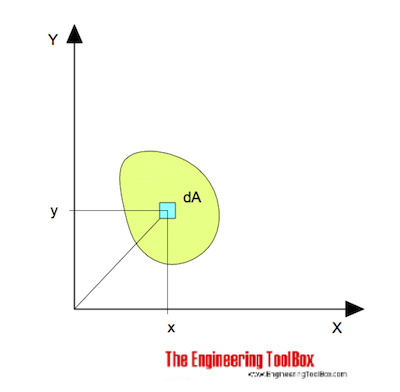
for bøyning rundt x – aksen kan uttrykkes som

Ix = ∫ y2 dA (1)

der

Ix = Område Treghetsmoment relatert til x-aksen (m4, mm4, inches4)

y = Den Vinkelrette avstanden Fra Akse X Til Elementet Da (m, Mm, Tommer)

dA = et elementært område (m2, mm2, inches2)

Momentet Av Treghet for bøyning rundt y – aksen kan uttrykkes som

iy = ∫ x2 dA (2)

hvor

Iy = Arealmoment Av Treghet relatert til y-aksen (m4, mm4, inches4)

x = vinkelrett avstand fra aksen y til elementet dA (m, mm, tommer)

Arealmoment Av Treghet for typisk tverrsnitt i

• område treghetsmoment for typiske tverrsnitt ii

solid kvadratisk tverrsnitt

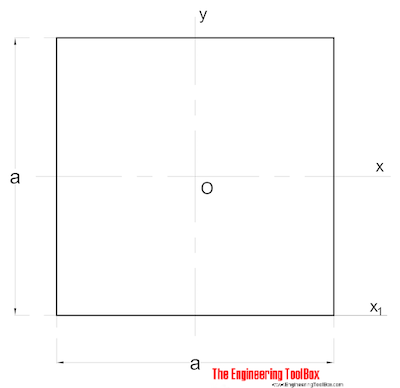
området treghetsmoment for en solid firkantet seksjon kan beregnes som

Ix = a4 / 12 (2)

hvor

a = side (mm, m, inn..)

Iy = a4 / 12 (2b)

Solid Rektangulært Tverrsnitt

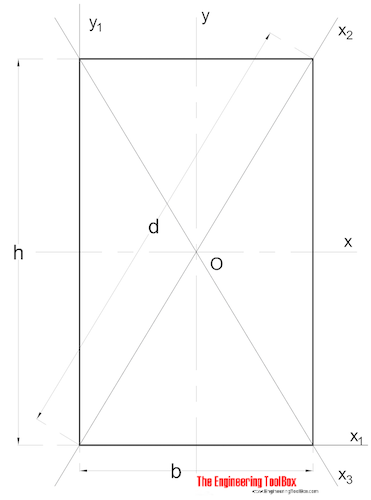
Inerias Områdemoment for en rektangulær seksjon kan beregnes som

Ix = b h3 / 12 (3)

hvor

b = bredde

h = høyde

Iy = b3 h / 12 (3b)

Solid Sirkulært Tverrsnitt

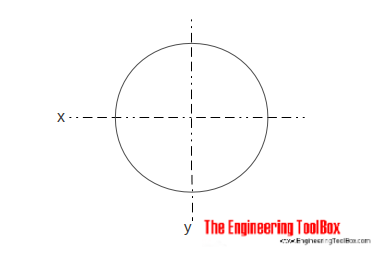
Treghet I Området for en solid sylindrisk seksjon kan beregnes som

ix = π r4 /4

= π d4 / 64 (4)

hvor

r = radius

d = diameter

Iy = π r4 / 4

= π d4 / 64 (4b)

Hul Sylindrisk Tverrsnitt

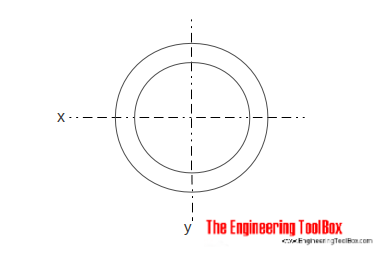
Treghet I Området for et hul sylindrisk tverrsnitt kan beregnes som

Ix = π (do4 – di4) / 64 (5)

hvor

do = sylinder utvendig diameter

di = sylinder innvendig diameter

iy = π (do4 – di4) / 64 (5b)

Kvadratisk Seksjon – Diagonale Moments

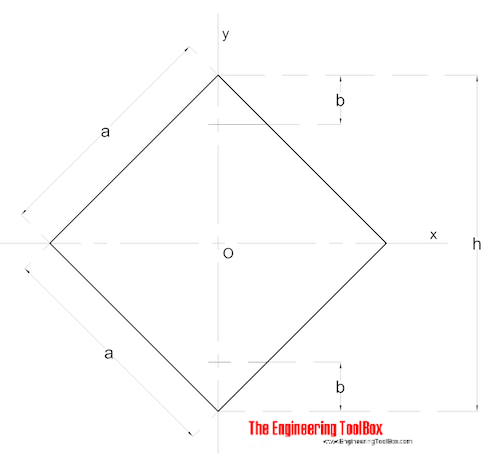
de diagonale Området Moments Of Inerti for en firkantet seksjon kan beregnes som

Ix = Iy = a4 / 12 (6)

Rektangulært Snitt – Områdemomenter På en hvilken som helst linje Gjennom Tyngdepunktet

Rektangulært snitt og Momentområde på linje Gjennom Tyngdepunktet kan beregnes som

Ix = (b h / 12) (h2 cos2 a + b2 sin2 a) (7)

Symmetrisk Form

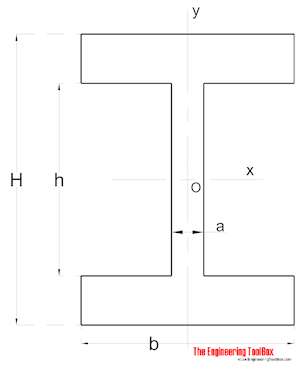
Treghetsmoment For En symmetrisk formet seksjon kan beregnes som

Ix = (a h3 / 12) + (b / 12) (H3 – h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

Ikke – Symmetrisk Form

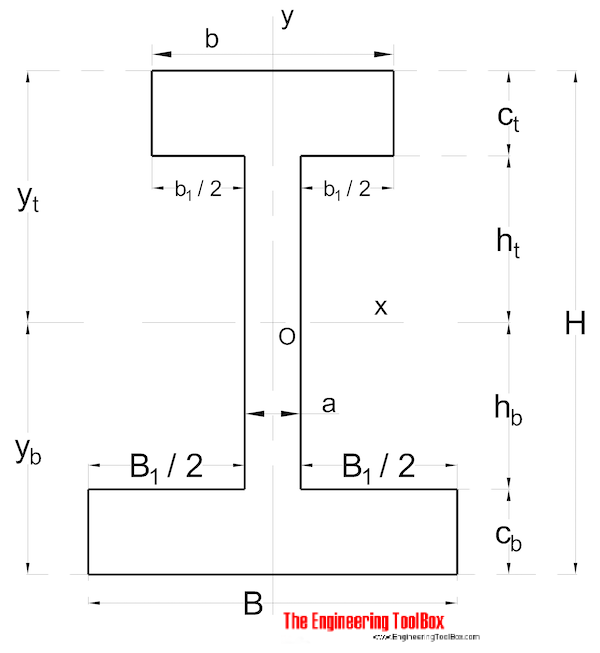
Område Treghetsmoment for en ikke-symmetrisk formet seksjon kan beregnes som

Ix = (1 / 3) (B Yb3-b1 hb3 + b yt3-b1 ht3) (9)

• Område Treghetsmoment for typiske Tverrsnitt II

Område Treghetsmoment vs. Polar Treghetsmoment vs. Moment Av Treghet

• «Område Treghetsmoment» Er en egenskap av form som brukes til å forutsi avbøyning, bøyning og stress i bjelker
• » Polar Treghetsmoment»som et mål på en stråles evne til å motstå torsjon – som er nødvendig for å beregne vridningen av en stråle utsatt for dreiemoment
• «Treghetsmoment» er et mål på et objekts motstand mot endring i rotasjonsretningen.

Seksjonsmodul

• «Seksjonsmodulen» er definert Som W = i / y, hvor jeg Er Områdets Treghetsmoment og y er avstanden fra den nøytrale aksen til en gitt fiber