
















Timsort: en veldig rask, O (n log n), stabil sorteringsalgoritme bygget for den virkelige verden – ikke konstruert i akademia.
Klikk her for å se den oppdaterte artikkelen:

Timsort Er en sorteringsalgoritme som er effektiv for virkelige data og ikke opprettet i et akademisk laboratorium. Tim Peters opprettet Timsort For Programmeringsspråket Python i 2001. Timsort analyserer først listen den prøver å sortere og velger deretter en tilnærming basert på analysen av listen.
siden algoritmen er oppfunnet, har den blitt brukt som standard sorteringsalgoritme i Python, Java, Android-Plattformen og I GNU Octave.
Timsorts store o-notasjon er O (n log n). For Å lære Om Big o notasjon, les dette.

Timsorts sorteringstid er den samme Som Mergesort, som er raskere enn de fleste andre typer du kanskje vet. Timsort faktisk gjør bruk Av Innsetting sortering og Mergesort, som du vil se snart.
Peters designet Timsort for å bruke allerede bestilte elementer som finnes i de fleste virkelige datasett. Det kaller disse allerede bestilte elementene «naturlige løp». Den iterates over dataene som samler elementene i løp og samtidig fusjonerer disse løpene sammen til en.
matrisen har færre enn 64 elementer i den
Hvis matrisen vi prøver å sortere har færre enn 64 elementer i Den, Utfører Timsort en innsettingssortering.
en innsettingssortering er en enkel sortering som er mest effektiv på små lister. Det er ganske treg på større lister, men veldig fort med små lister. Ideen om en innsettingssortering er som følger:
- Se på elementer en etter en
- Bygg opp sortert liste ved å sette inn elementet på riktig sted
Her er en sporingstabell som viser hvordan innsettingssortering ville sortere listen

I dette tilfellet setter vi inn de nysorterte elementene i en ny undergruppe, som starter ved starten av arrayet.
her er en gif som viser innsettingssortering:
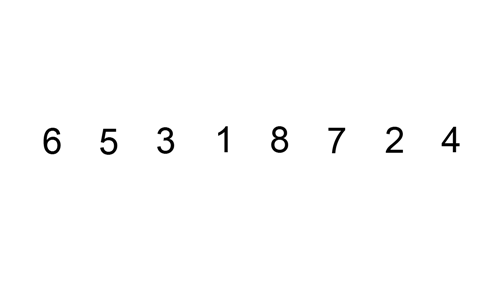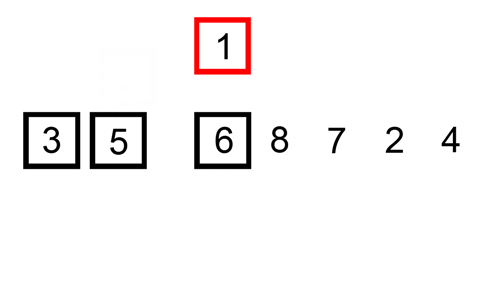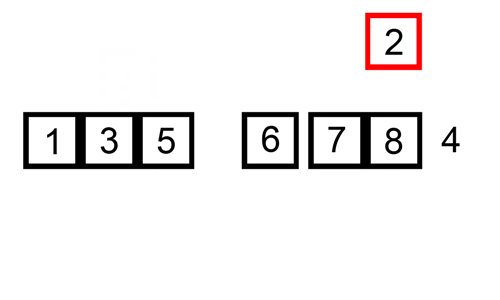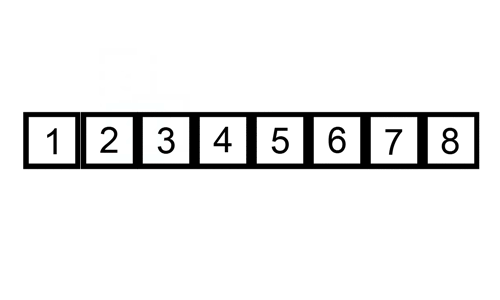
Mer om runs
hvis listen er større enn 64 elementer enn algoritmen vil gjøre en første passering gjennom listen på jakt etter deler som er strengt økende eller avtagende. Hvis delen er avtagende, vil den reversere den delen.
så hvis løp er avtagende, vil det se slik ut (hvor løp er i fet skrift):

hvis ikke avtagende, vil det se slik ut:

minrun er en størrelse som bestemmes ut fra størrelsen på arrayet. Algoritmen velger det slik at de fleste kjører i en tilfeldig matrise er, eller bli minrun, i lengde. Sammenslåing 2 arrays er mer effektiv når antall kjøringer er lik, eller litt mindre enn, en kraft på to. Timsort velger minrun for å prøve å sikre denne effektiviteten, ved å sørge for at minrun er lik eller mindre enn en kraft på to.
algoritmen velger minrun fra området 32 til 64 inkludert. Den velger minrun slik at lengden på den opprinnelige matrisen, når den deles med minrun, er lik eller litt mindre enn en kraft på to.
hvis lengden på kjøringen er mindre enn minrun, beregner du lengden på kjøringen fra minrun. Ved hjelp av dette nye nummeret tar du tak i mange elementer foran løp og utfører en innsettingssortering for å opprette en ny løp.
Så hvis minrun er 63 og lengden på løp er 33, gjør du 63-33 = 30. Du tar deretter 30 elementer fra foran slutten av løp, så dette er 30 elementer fra løp og deretter utføre en innsettingssortering for å opprette en ny løp.
etter at denne delen er fullført, skal vi nå ha en rekke sorterte løp i en liste.
Sammenslåing

Timsort utfører nå mergesort for å slå sammen løpene sammen. Timsort sørger imidlertid For å opprettholde stabilitet og flettebalanse mens flettesortering.
for å opprettholde stabilitet bør vi ikke bytte 2 tall av lik verdi. Dette holder ikke bare sine opprinnelige posisjoner i listen, men gjør det mulig for algoritmen å være raskere. Vi vil om kort tid diskutere flettebalansen.
Når Timsort finner kjører, legger Den dem til en stabel. En enkel stabel ville se slik ut:

Tenk deg en stabel med plater. Du kan ikke ta plater fra bunnen, så du må ta dem fra toppen. Det samme gjelder om en stabel.
Timsort prøver å balansere to konkurrerende behov når flergesort kjøres. På den ene siden ønsker vi å utsette sammenslåingen så lenge som mulig for å utnytte mønstre som kan komme opp senere. Men vi ønsker enda mer å gjøre sammenslåingen så snart som mulig for å utnytte løp som løpene nettopp fant, er fortsatt høyt i minnehierarkiet. Vi kan heller ikke forsinke sammenslåing «for lenge» fordi det bruker minne for å huske løpene som fortsatt er unmerged, og stakken har en fast størrelse.
For å sikre at Vi har dette kompromisset, Holder Timsort styr på de tre nyeste elementene i stabelen og oppretter to lover som må være sanne for disse elementene:
1. A > B + C
2. B > C
Der A, B Og C er de tre siste elementene på stakken.
I Ordene Til Tim Peters selv:
det som viste seg å være et godt kompromiss opprettholder to invariants på stabeloppføringene, Hvor A, B og C er lengdene til de tre høyre ikke-sammenslåtte skivene
vanligvis er det vanskelig å slå sammen tilstøtende løp av forskjellige lengder på plass. Det som gjør det enda vanskeligere er at vi må opprettholde stabiliteten. For å komme seg rundt dette, Setter Timsort midlertidig minne. Den plasserer den mindre (kaller begge kjører A Og B) av de to går inn i det midlertidige minnet.
Galopperende

Mens Timsort fusjonerer A Og B, merker Det at en løp har «vunnet» mange ganger på rad. Hvis det viste seg at løp a besto av helt mindre tall Enn løp B, ville løp A ende opp igjen på sin opprinnelige plass. Sammenslåing av de to løpene ville innebære mye arbeid for å oppnå ingenting.
oftere enn ikke, vil data ha noen eksisterende intern struktur. Timsort antar at hvis mange run a-verdier er lavere enn run B-verdier, er Det sannsynlig At A vil fortsette å ha mindre verdier Enn B.
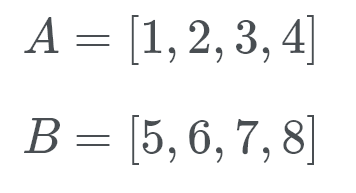
Timsort vil da gå inn i galopperende modus. I stedet for å sjekke A og B mot hverandre, Utfører Timsort et binært søk etter riktig posisjon av b i a. På Denne måten Kan Timsort flytte en hel del Av A på plass. Da Timsort søker etter riktig plassering Av A I B. Timsort vil da flytte en hel del Av b kan på en gang, og på plass.
La oss se dette i aksjon. Timsort sjekker B (som er 5) og bruker et binært søk det ser etter riktig sted I A.
Vel, b tilhører på baksiden av listen Over A. Nå Timsort sjekker For A (som er 1)i riktig plassering Av B. så vi ønsker å se hvor nummer 1 går. Dette tallet går i starten Av B. Vi vet nå At B tilhører på slutten Av A og a tilhører i starten Av B.
det viser seg at denne operasjonen ikke er verdt det hvis riktig sted For B er svært nær begynnelsen Av A (eller omvendt). så galoppmodus går raskt ut hvis det ikke lønner seg. I Tillegg Tar Timsort notat og gjør det vanskeligere å gå inn i galoppmodus senere ved å øke antall påfølgende A – only eller B-only wins som kreves for å delta. Hvis galoppmodus lønner seg, Gjør Timsort det lettere å oppgi.
Kort Sagt, Timsort gjør 2 ting utrolig bra:
- Flott ytelse på arrays med eksisterende intern struktur
- Å kunne opprettholde en stabil sortering
Tidligere, For å oppnå en stabil sortering, må du zip elementene i listen din opp med heltall, og sortere den som en rekke tuples.
Kode
hvis du ikke er interessert i koden, kan du hoppe over denne delen. Det er litt mer informasjon under denne delen.
kildekoden nedenfor er basert på mine Og Nanda Javarmas arbeid. Kildekoden er ikke komplett, og den ligner heller Ikke Pythons offisielle sorterte () kildekode. Dette er bare en dumbed-down Timsort jeg implementert for å få en generell følelse Av Timsort. Hvis Du vil se Timsorts originale kildekode i all sin herlighet, sjekk den ut her. Timsort er offisielt implementert I C, ikke Python.
Timsort er faktisk bygget rett inn I Python, så denne koden fungerer bare som en forklarer. For Å bruke Timsort bare skrive:
list.sort()
Eller
sorted(list)
Hvis Du vil mestre Hvordan Timsort fungerer og få en følelse for Det, foreslår jeg at du prøver å implementere det selv!
denne artikkelen er basert På Tim Peters ‘ opprinnelige introduksjon Til Timsort, funnet her.