Logaritmen: Inleiding tot “de relatie”

Return to the Lessons Index / Do the Lessons in Order / Print-friendly page

logaritmen: Inleiding tot
” the Relationship “(pagina 1 van 3)

secties: Inleiding tot logboeken, vereenvoudiging van loguitdrukkingen, gemeenschappelijke en natuurlijke logboeken

logaritmen zijn het” tegenovergestelde ” van exponentialen, net zoals Aftrekken het tegenovergestelde is van optellen en delen het tegenovergestelde is van vermenigvuldigen. Logs “ongedaan maken” exponentials. Technisch gesproken zijn logboeken de inverse van exponentialen.

in praktische termen heb ik het nuttig gevonden om logs te zien in termen van de relatie:

aan de linkerkant hierboven is de exponentiële verklaring “y = bx”. Aan de rechterkant hierboven is “logb(y) = x” het equivalente logaritmische statement, dat uitgesproken wordt als “log-base-b van y is gelijk aan x”; de waarde van het subscript “b” is “de basis van de logaritme”, net zoals b de basis is in de exponentiële uitdrukking “bx”. En, net zoals de basis b in een exponentieel altijd positief is en niet gelijk aan 1, zo is ook de basis b voor een logaritme altijd positief en niet gelijk aan 1. Wat zich in de logaritme bevindt wordt het “argument” van de log genoemd. Merk op dat de basis in zowel de exponentiële vergelijking als de logvergelijking (hierboven) “b” is, maar dat de x en y van kant wisselen wanneer je tussen de twee vergelijkingen wisselt.

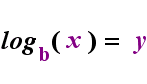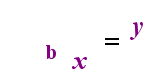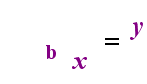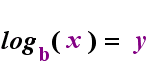
als je je deze relatie kunt herinneren (dat wat het argument van de log geweest is de “gelijken” wordt en wat de “gelijken” was wordt de exponent in de exponentiële, en vice versa), dan zou je niet al te veel moeite moeten hebben met logaritmen.

(ik heb zelf de term “de relatie” bedacht. Je zult het niet vinden in je tekst, en je leraren en docenten zullen geen idee hebben waar je het over hebt als je het tegen hen zegt. “De relatie” is volledig niet-standaard terminologie. Waarom gebruik ik het eigenlijk? Omdat het werkt.)

Trouwens: als je gemerkt hebt dat ik de variabelen heb verwisseld tussen de twee kaders die “de relatie” weergeven, heb je een scherp oog. Ik deed dat met opzet, om te benadrukken dat het niet om de variabelen zelf gaat, maar om hoe ze bewegen.

• converteer “63 = 216” naar de equivalente logaritmische uitdrukking.

om te converteren, de basis (dat wil zeggen, de 6)blijft hetzelfde, maar de 3 en de 216 schakelaar zijden. Dit geeft me:

log6 (216) = 3 Copyright © Elizabeth Stapel 2002-2011 Alle rechten voorbehouden

• converteer “log4 ( 1024) = 5” naar de equivalente exponentiële expressie.

om te converteren, de basis (dat wil zeggen, de 4) blijft hetzelfde, maar de 1024 en de 5 schakelaar zijden. Dit geeft me:

45 = 1024

boven| 1 | 2 | 3 | terug naar Index>>