
















Timsort: een zeer snel, o (n log n), stabiel sorteeralgoritme gebouwd voor de echte wereld — niet gebouwd in de academische wereld.
Klik hier om het bijgewerkte artikel te bekijken:

Timsort is een sorteeralgoritme dat efficiënt is voor real-world data en niet is gemaakt in een academisch laboratorium. Tim Peters creëerde Timsort voor de programmeertaal Python in 2001. Timsort analyseert eerst de lijst die het probeert te sorteren en kiest vervolgens een aanpak op basis van de analyse van de lijst.
sinds het algoritme is uitgevonden, wordt het gebruikt als standaard sorteeralgoritme in Python, Java, het Android-Platform en in GNU Octave.
Timsort ‘ s big O notatie is O (n log n). Lees dit voor meer informatie over Big O notatie.

de sorteertijd van Timsort dezelfde als Mergesort, wat sneller is dan de meeste andere soorten die u kent. Timsort maakt eigenlijk gebruik van Insertion sort en Mergesort, zoals je snel zult zien.
Peters ontwierp Timsort om reeds geordende elementen te gebruiken die in de meeste reële datasets voorkomen. Het noemt deze reeds geordende elementen “natuurlijke runs”. Het itereert over de gegevens verzamelen van de elementen in runs en tegelijkertijd samenvoegen die loopt samen in een.
de array bevat minder dan 64 elementen
als de array die we proberen te sorteren minder dan 64 elementen bevat, zal Timsort een invoegsort uitvoeren.
een invoegsoort is een eenvoudige soort die het meest effectief is op kleine lijsten. Het is vrij traag op grotere lijsten, maar zeer snel met kleine lijsten. Het idee van een insertion sort is als volgt:
- bekijk elementen één voor één
- gesorteerde lijst opbouwen door het element op de juiste locatie in te voegen
hier is een trace table die laat zien hoe invoegsorteer de lijst zou Sorteren

in dit geval voegen we de nieuw gesorteerde elementen in een nieuwe sub-array, die begint bij het begin van de array.
hier is een gif die invoegsorteert:
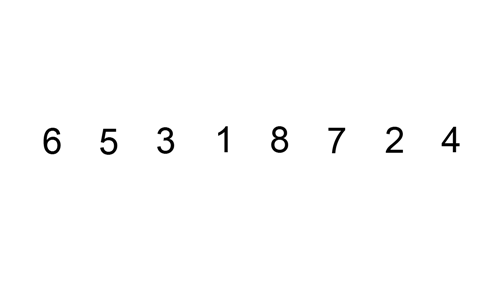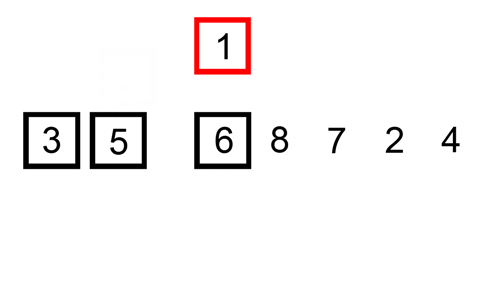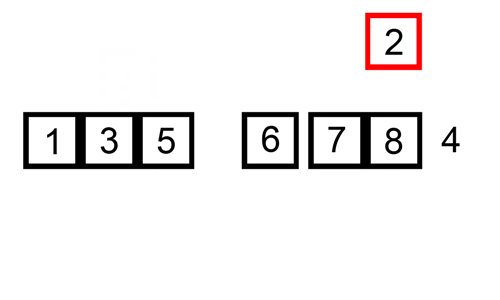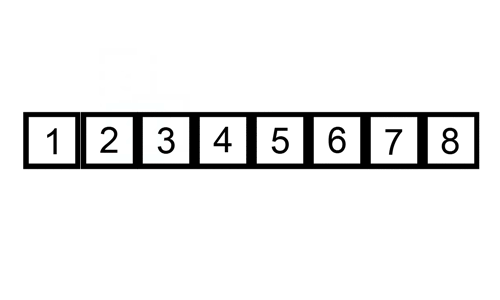
meer over runs
als de lijst groter is dan 64 elementen dan zal het algoritme een eerste door de lijst gaan op zoek naar delen die strikt toenemen of afnemen. Als het deel afneemt, zal het dat deel omkeren.
dus als de run afneemt, ziet deze er zo uit (waarbij de run vet is):

als het niet afneemt, ziet het er zo uit:

de minrun is een grootte die wordt bepaald op basis van de grootte van de array. Het algoritme selecteert het zo dat de meeste runs in een willekeurige array zijn, of worden minrun, in lengte. Het samenvoegen van 2 arrays is efficiënter wanneer het aantal runs gelijk is aan, of iets minder is dan, een macht van twee. Timsort kiest minrun om te proberen deze efficiëntie te garanderen, door ervoor te zorgen dat minrun gelijk is aan of kleiner is dan een kracht van twee.
het algoritme kiest minrun uit het bereik 32 tot en met 64. Het kiest minrun zodanig dat de lengte van de originele array, gedeeld door minrun, gelijk is aan of iets minder dan een macht van twee.
als de lengte van de run kleiner is dan minrun, berekent u de lengte van die run weg van minrun. Met behulp van dit nieuwe nummer, Je pakt dat veel items voorafgaand aan de run en het uitvoeren van een invoegsorteerfunctie om een nieuwe run te maken.
dus als minrun 63 is en de lengte van de run 33 is, doe je 63-33 = 30. U pakt dan 30 elementen van voor het einde van de run, dus dit is 30 items van run en voer vervolgens een invoegsorteerfunctie uit om een nieuwe run te maken.
nadat dit deel is voltooid zouden we nu een aantal gesorteerde runs in een lijst moeten hebben.
samenvoegen

Timsort voert nu mergesort uit om de runs samen te voegen. Timsort zorgt er echter voor dat de stabiliteit behouden blijft en de balans samenvoegt tijdens het sorteren.
om de stabiliteit te behouden moeten we geen 2 getallen van gelijke waarde uitwisselen. Dit houdt niet alleen hun oorspronkelijke posities in de lijst, maar maakt het algoritme sneller. We zullen binnenkort de fusiebalans bespreken.
als Timsort runs vindt, voegt het ze toe aan een stack. Een eenvoudige stapel zou er zo uitzien:

stel je een stapel platen voor. Je kunt geen platen van de bodem nemen, dus je moet ze van de bovenkant nemen. Hetzelfde geldt voor een stapel.
Timsort probeert twee concurrerende behoeften in evenwicht te brengen wanneer mergesort wordt uitgevoerd. Aan de ene kant willen we het samenvoegen zo lang mogelijk uitstellen om patronen te benutten die later naar voren kunnen komen. Maar we zouden nog meer willen doen het samenvoegen zo snel mogelijk om de run die de run net gevonden is nog steeds hoog in de geheugenhiërarchie te benutten. We kunnen het samenvoegen van “te lang” ook niet uitstellen omdat het geheugen verbruikt om de runs te onthouden die nog niet zijn samengevoegd, en de stack een vaste grootte heeft.
om er zeker van te zijn dat we dit compromis hebben, houdt Timsort de drie meest recente items op de stack bij en creëert twee wetten die waar moeten zijn voor deze items:
1. A > B + C
2. B > C
waarbij A, B en C de drie meest recente items op de stack zijn.
in de woorden van Tim Peters zelf:
wat een goed compromis bleek te zijn, handhaaft twee invarianten op de stack entries, waar A, B en C de lengtes zijn van de drie meest rechtse niet-nog samengevoegde slices
Gewoonlijk is het samenvoegen van aangrenzende runs van verschillende lengtes op hun plaats moeilijk. Wat het nog moeilijker maakt is dat we stabiliteit moeten handhaven. Om dit te omzeilen, zet Timsort tijdelijk geheugen opzij. Het plaatst de kleinere (die beide runs a en B aanroept) van de twee runs in dat tijdelijke geheugen.
galopperen

terwijl Timsort A en B samenvoegt, merkt het dat één run vele malen achter elkaar” winnende ” is geweest. Als zou blijken dat de run a bestond uit geheel kleinere getallen dan de run B dan zou de run A weer op zijn oorspronkelijke plaats. Het samenvoegen van de twee runs zou veel werk vergen om niets te bereiken.
vaak hebben gegevens een reeds bestaande interne structuur. Timsort gaat ervan uit dat als veel run A ‘S waarden lager zijn dan run B’ s waarden, dan is het waarschijnlijk dat A kleinere waarden zal blijven hebben dan B.
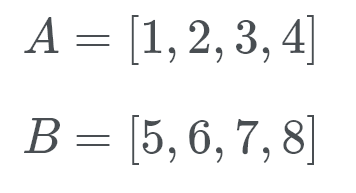
Timsort zal dan galopperen. In plaats van A en B tegen elkaar te controleren, voert Timsort een binaire zoekopdracht uit naar de juiste positie van b in a. op deze manier kan Timsort een hele sectie van A op zijn plaats zetten. Dan zoekt Timsort naar de juiste locatie van A in B. Timsort zal dan een hele sectie van B kan in een keer verplaatsen, en op zijn plaats.
laten we dit in actie zien. Timsort checkt B (dat is 5) en met behulp van een binaire zoekopdracht zoekt het naar de juiste locatie in A.
nou, B hoort aan de achterkant van de lijst van A. Nu controleert Timsort voor A (dat is 1) op de juiste locatie van B. Dus we kijken om te zien waar het nummer 1 gaat. Dit getal staat aan het begin van B. We weten nu dat B aan het eind van A hoort en A aan het begin van B.
het blijkt dat deze operatie niet de moeite waard is als de juiste locatie voor B heel dicht bij het begin van A ligt (of vice versa). dus galop modus verlaat snel als het niet loont. Daarnaast neemt Timsort er nota van en maakt het moeilijker om later in de galopmodus te komen door het aantal opeenvolgende A-alleen of B-alleen overwinningen te verhogen. Als de galopmodus zijn vruchten afwerpt, maakt Timsort het makkelijker om opnieuw in te gaan.
kortom, Timsort doet 2 dingen ongelooflijk goed:
- geweldige prestaties op arrays met een reeds bestaande interne structuur
- in staat zijn om een stabiele sorteerwaarde
te behouden voordat u een stabiele sorteerwaarde wilt bereiken, moet u de items in uw lijst met gehele getallen zippen en sorteren als een array van tupels.
Code
als u niet geïnteresseerd bent in de code, kunt u dit gedeelte overslaan. Er is wat meer informatie onder deze sectie.
onderstaande broncode is gebaseerd op het werk van mijn en Nanda Jaharma. De broncode is niet compleet, noch is het vergelijkbaar met Python ‘ s officiële gesorteerde () broncode. Dit is gewoon een dumbed-down Timsort die ik heb geïmplementeerd om een algemeen gevoel van Timsort te krijgen. Als je de originele broncode van Timsort in al zijn glorie wilt zien, bekijk het hier. Timsort is officieel geïmplementeerd in C, niet Python.
Timsort is eigenlijk ingebouwd in Python, dus deze code dient alleen als een uitleg. Om Timsort te gebruiken schrijf gewoon:
list.sort()
of
sorted(list)
Als u wilt beheersen hoe Timsort werkt en krijg een gevoel voor het, Ik stel voor dat u probeert om het zelf uit te voeren!
dit artikel is gebaseerd op Tim Peters’ oorspronkelijke inleiding tot Timsort, hier te vinden.