gdzie jest funkcja w punkcie wysokim lub niskim? Rachunek może pomóc!
maksimum to wysoki punkt, a minimum to niski punkt:
w płynnie zmieniającej się funkcji maksimum lub minimum jest zawsze tam, gdzie funkcja spłaszcza się (z wyjątkiem punktu siodła).
gdzie to się spłaszcza? Gdzie nachylenie jest zerowe.
gdzie jest nachylenie zero? Pochodna mówi nam!
zanurkujmy z przykładem:
- przykład: piłka jest wyrzucana w powietrze. Jego wysokość w dowolnym momencie T jest podana przez:
- jaka jest jego maksymalna wysokość?
- szybkie odświeżanie pochodnych
- skąd wiemy, że jest to maksimum (lub Minimum)?
- Test drugiej pochodnej
- przykład: Znajdź maksima i minima dla:
- wyrazy
- jeszcze jeden przykład
- przykład: Znajdź maksima i minima dla:
- musi być różny
- przykład: a co z funkcją f (x) = / x / (wartość bezwzględna) ?
przykład: piłka jest wyrzucana w powietrze. Jego wysokość w dowolnym momencie T jest podana przez:
h = 3 + 14T-5t2
jaka jest jego maksymalna wysokość?
używając pochodnych możemy znaleźć nachylenie tej funkcji:
![]() h = 0 + 14 − 5(2T)
h = 0 + 14 − 5(2T)
= 14 − 10T
(zobacz poniżej ten przykład, jak znaleźliśmy tę pochodną.)
teraz znajdź, gdy nachylenie jest zerowe:
nachylenie wynosi zero Przy t = 1,4 sekundy
, a wysokość w tym czasie wynosi:
i tak:
maksymalna wysokość to 12,8 m (Przy t = 1,4 s)
szybkie odświeżanie pochodnych
pochodna zasadniczo znajduje nachylenie funkcji.
w poprzednim przykładzie wzięliśmy to:
h = 3 + 14T-5t2
i wymyśliliśmy tę pochodną:
![]() h = 0 + 14 − 5 (2T)
h = 0 + 14 − 5 (2T)
= 14 − 10T
, który podaje nam nachylenie funkcji w dowolnym momencie t
użyliśmy tych zasad pochodnych:
- nachylenie stałej wartości (np. 3) wynosi 0
- nachylenie linii jak 2x wynosi 2, więc 14T ma nachylenie 14
- funkcja kwadratowa jak t2 ma nachylenie 2T, więc 5T2 ma nachylenie 5 (2T)
- a następnie dodaliśmy je: 0 + 14 − 5 (2t)
skąd wiemy, że jest to maksimum (lub Minimum)?
widzieliśmy to na wykresie! Ale inaczej … pochodne znów przychodzą na ratunek.
Weźmy pochodną nachylenia (druga pochodna pierwotnej funkcji):
Pochodna 14 − 10t wynosi -10
oznacza to, że nachylenie jest stale zmniejszane (-10): podróżując od lewej do prawej nachylenie zaczyna się dodatnio (funkcja wzrasta), przechodzi przez zero (punkt płaski), a następnie nachylenie staje się ujemne (funkcja spada).:

nachylenie, które staje się mniejsze (i przechodzi przez 0) oznacza maksimum.
nazywa się to drugim testem pochodnym
na powyższym wykresie pokazałem nachylenie przed i po, ale w praktyce wykonujemy test w punkcie, w którym nachylenie jest zerowe:
Test drugiej pochodnej
gdy nachylenie funkcji wynosi zero w punkcie x, a druga pochodna w punkcie x wynosi:
- mniej niż 0, jest to lokalne maksimum
- większe niż 0, jest to lokalne minimum
- równe 0 ,wtedy test nie powiedzie się (mogą być inne sposoby sprawdzenia)
„druga pochodna: mniejsza od 0 to maksimum, większa od 0 to minimum”
przykład: Znajdź maksima i minima dla:
y = 5×3 + 2×2-3x
pochodna (nachylenie) wynosi:
![]() y = 15×2 + 4x− 3
y = 15×2 + 4x− 3
który jest kwadratowy z zerami na:
- x = -3/5
- x = +1/3
czy mogą to być maxima czy minima? (Nie patrz jeszcze na wykres!)
druga pochodna to y „= 30x + 4
przy x = -3/5:
W x = +1/3:
(teraz możesz spojrzeć na wykres.)
wyrazy
wysoki punkt nazywa się maksimum (liczba mnoga maxima).
niski punkt nazywa się minimum (minima w liczbie mnogiej).
ogólne słowo oznaczające maksimum lub minimum to extremum (liczba mnoga extrema).
mówimy lokalne maksimum (lub minimum), gdy mogą być wyższe (lub niższe) punkty w innym miejscu, ale nie w pobliżu.
jeszcze jeden przykład
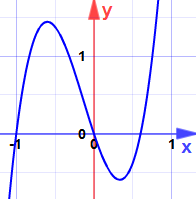
przykład: Znajdź maksima i minima dla:
y = x3 − 6×2 + 12x − 5
pochodna to:
![]() y = 3×2 − 12x + 12
y = 3×2 − 12x + 12
który jest kwadratowy z jednym zerem przy x = 2
czy jest to maksimum czy minimum?
druga pochodna to y „= 6x-12
przy x = 2:
i oto dlaczego:
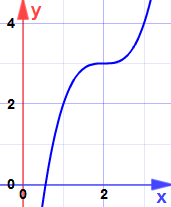
jest to punkt siodłowy … nachylenie staje się zerowe, ale nie jest ani maksimum, ani minimum.
musi być różny
i jest ważny punkt techniczny:
funkcja musi być różniczkowalna (pochodna musi istnieć w każdym punkcie swojej dziedziny).
przykład: a co z funkcją f (x) = / x / (wartość bezwzględna) ?
| |x / wygląda tak: |  |
Przy x=0 ma bardzo ostrą zmianę!
w rzeczywistości nie jest tam różnicowalny (jak pokazano na stronie różnicowalnej).
więc nie możemy użyć tej metody dla funkcji wartości bezwzględnej.
funkcja musi być również ciągła, ale każda funkcja, która jest różniczkowalna, jest również ciągła, więc nie musisz się o to martwić.



