Se o nosso objectivo é encontrar a generalização relativística de Poisson ‘s equação para o campo gravitacional:
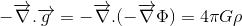
onde Φ refere-se ao potencial gravitacional e ρ a densidade de massa, estamos no meio do caminho.
na verdade, já vimos em nosso artigo anterior o tensor energia-momento que a generalização da densidade de massa (termo da mão direita da equação) corresponde ao energia-momento Tµv.
parece razoável, então, supor que a nossa equação deve assumir a forma de:
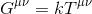
onde k é um escalar e Gµv, o chamado tensor de Einstein representa um rank-2 tensor de descrever o espaço-tempo com curvatura .
tanto quanto sabemos, os Gµv devem obedecer às seguintes restrições::
– deve anular no plano espaço-tempo
– deve descrever o espaço-tempo com curvatura e ser linear com relação ao de Riemann
– deve ser simétrico e de rank 2 (como Tµv)
– ele deve ter um valor nulo divergência (como Tµv)
– e, finalmente, em Newtoniana limites, ele deve reduzir a 4nGp
Primeira tentativa com o tensor de Ricci como solução
lembramos de nosso artigo Geodésica equação Newtoniana Limite que o potencial gravitacional Φ é ligada à 00-componente da métrica através h00=(g00-1)/c2
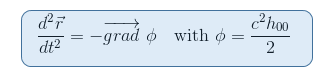
parece então natural procurar um tensor que envolve os segundos derivados da métrica, que é o caso do tensor de Riemann. Além disso, o tensor de Riemann é o único candidato que sabemos até agora para ser capaz de descrever a curvatura do espaço-tempo (cf segunda restrição acima).Como temos de encontrar um tensor rank-2, e se assumirmos que temos de encontrar uma solução apenas em termos do tensor de Riemann, parece natural considerar primeiro a forma contratada do tensor de Riemann, conhecido como tensor de Ricci.
Para ver isso, vamos relembrar a expressão do tensor de Riemann de tha artigo Riemann curvatura de riemann parte II: cálculo do desvio geodésico
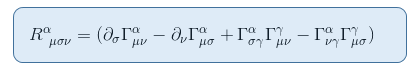
No limite de um estático e fraco campo gravitacional, apenas um termo contribui para R00:
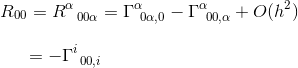
No mesmo artigo, calculou-se este símbolo de Christoffel e descobriu que
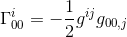
com a aproximação do gij = nij e goo,j = hoo,j (veja o artigo) obtemos:
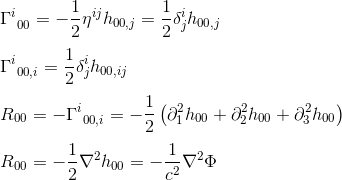
a identificação de R00 Com ΔΦ (operador Laplaciano) sugere que a equação de campo na relatividade geral deve igualar Rab a um múltiplo constante de Tab.
Em 1915, usando esta equação, Einstein era mesmo capaz de resolver o problema de longa data de Mercúrio precessão do periélio, fazendo com que, para escrever, em novembro do mesmo ano, que, “Por alguns dias, eu estava fora de mim com alegre entusiasmo.”
eventualmente, Einstein teve que rejeitar esta primeira tentativa, devido ao fato de que na divergência geral de Rab não anula.
segunda tentativa
há um tensor intimamente relacionado com o wihch escalar de Ricci pode ser colocado no lado esquerdo sem contradição. Isto dá o tensor de Einstein definido da seguinte forma::
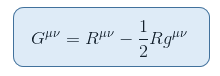
onde R = Raa é a curvatura Scalar Ricci ou scalar.
esta forma de Gab é simétrica e de rank-2 e obviamente descreve a curvatura do espaço-tempo. Então, ele permanece apenas para mostrar que o total derivada é zero
Para fazer isso, vamos começar com a identidade de Bianchi
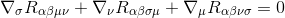
Multiplicando-se através de gγσgαμgβν (métricas derivativos são zero, então eles agem como constantes e pode ser levado dentro de derivativos), que produz a:
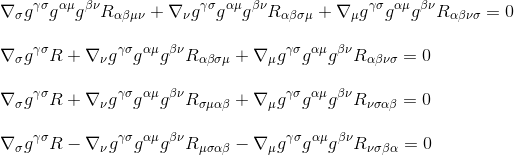
utilizando o tensor de Ricci definição Rµv=gμβgνσRβσ (passo 3) e renomeando os índices (passo 4), obtemos
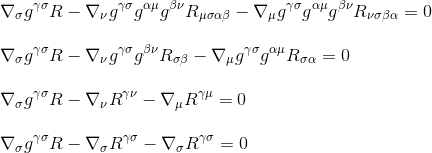
Por factorising a derivada, podemos finalmente obter
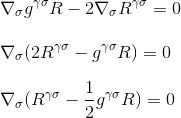
o que é exatamente o que nós queríamos demonstrar: a divergência do tensor de Einstein é nulo, e nós encontramos o candidato certo para o lado esquerdo do nosso curvatura/massa-equação de energia.