Voltar para as Aulas de Índice | Fazer as Lições na Ordem | Imprimir página
Logaritmos: Introdução
“Relação” (página 1 de 3)
Seções: Introdução aos registos, a Simplificar o registo de expressões, Comuns e naturais logs
Logaritmos são o “oposto” de exponenciais, assim como a subtração é o oposto de adição e divisão é o oposto da multiplicação. Regista os exponenciais “desfazer”. Tecnicamente falando, os logs são os inversos dos exponenciais.
Em termos práticos, tem-me sido útil para pensar de logs em termos de Relacionamento:
| —O Relacionamento— | |||
|
No lado esquerdo acima é exponencial da instrução “y = bx”. No lado direito, acima, “logb(y) = x” é o equivalente logarítmica instrução, que é pronunciado “log-base-b de y é igual a x”; O valor da subscritos “b” é “a base do logaritmo”, assim como b é a base da exponencial expressão “bx”. E, assim como a base b em um exponencial é sempre positiva e não igual a 1, também a base b para um logaritmo é sempre positiva e não igual a 1. O que quer que esteja dentro do logaritmo é chamado de “argumento” do log. Note que a base tanto na equação exponencial quanto na equação log (acima) é “b”, mas que o X e y trocam de lado quando você troca entre as duas equações.
—A Relação de Animação—
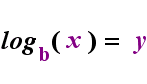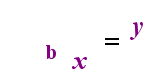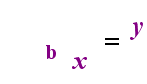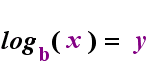
Se você pode lembrar-se desse relacionamento (que tudo o que tinha sido o argumento do registo torna-se o “igual”, e tudo o que tinha sido o “iguais” torna-se o expoente da exponencial, e vice-versa), em seguida, você não deve ter muitos problemas com logaritmos.
(eu próprio inventei o termo “a relação”. Você não vai encontrá-lo em seu texto, e seus professores e tutores não terão nenhuma idéia do que você está falando se você mencioná-lo a eles. “A relação” é uma terminologia totalmente não-padrão. Porque é que o uso? Porque funciona.)
a propósito: Se você notou que eu troquei as variáveis entre as duas caixas mostrando “a relação”, você tem um olho afiado. Fi-lo de propósito, para salientar que a questão não são as próprias variáveis, mas a forma como se movem.
- Converter “63 = 216” para a expressão logarítmica equivalente.
para converter, a base (ou seja, o 6)permanece a mesma, mas os 3 e os 216 trocam de lado. Isso me dá:
log6(216) = 3 Copyright © Elizabeth Stapel 2002-2011 Todos os Direitos Reservados
- Converter “log4(1024) = 5” é equivalente a expressão exponencial.
para converter, a base (isto é, o 4) permanece a mesma, mas os 1024 e os 5 switch sides. Isto dá-me:
45 = 1024
Topo| 1 | 2 | 3 | Voltar ao Índice Próximo >>
|
Citar este artigo como: |
Stapel, Elizabeth. “Logarithms: Introduction to ‘the Relationship’.”Purplemath. Disponível em 2016
|