Momento de inércia – secções transversais típicas I

momento de inércia ou Momento de inércia para uma área – também conhecido como segundo momento de Área – I, é uma propriedade da forma que é usada para prever deflexão, flexão e tensão em vigas.

Área de Momento de Inércia – unidades Imperiais

• inches4

Área de Momento de Inércia – unidades Métricas

• mm4
• cm4
• m4

Conversão entre Unidades de

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4.16×105 mm4 = 41.6 cm4

exemplo-conversão entre o momento de inércia da área

9240 cm4 pode ser convertida em mm4 multiplicando-se por 104

(9240 cm4) 104 = 9.24 107 mm4

Área de Momento de Inércia Momento de Inércia de uma Área ou Segundo Momento de Área)

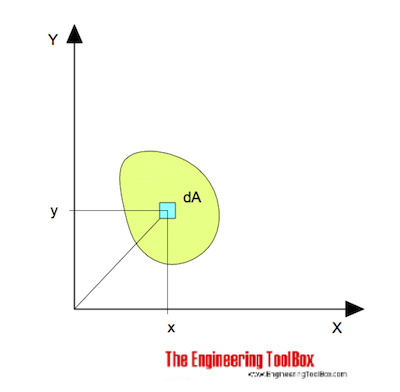
para flexão em torno do eixo x pode ser expresso como

Ix = ∫ y2 dA (1)

onde

Ix = Área de Momento de Inércia relacionadas com o eixo x (m4, mm4, inches4)

y = a distância perpendicular do eixo x para o elemento dA (m, mm, polegadas)

dA = de um elemental de área (m2, mm2, inches2)

O Momento de Inércia para flexão em torno do eixo y pode ser expressa como

Iy = ∫ x2 dA (2)

onde

Iy = Área de Momento de Inércia relacionadas com o eixo y (m4, mm4, inches4)

x = a distância perpendicular do eixo y para o elemento dA (m, mm, pol.)

Área de Momento de Inércia para uma típica Cruz Seções I

• Área de Momento de Inércia para uma típica Cruz Seções II

Sólida Seção Transversal Quadrada

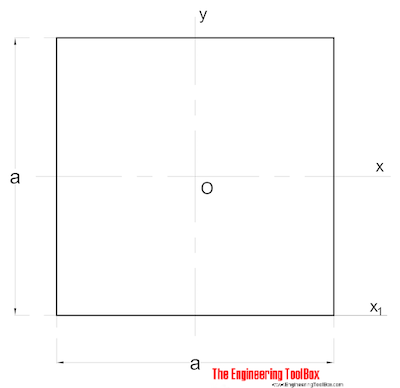
A Área de Momento de Inércia de um sólido de secção quadrada pode ser calculado como

Ix = a4 / 12 (2)

em que

a = lado (mm, m, in..)

Iy = a4 / 12 (2b)

Sólida de Seção Transversal Retangular

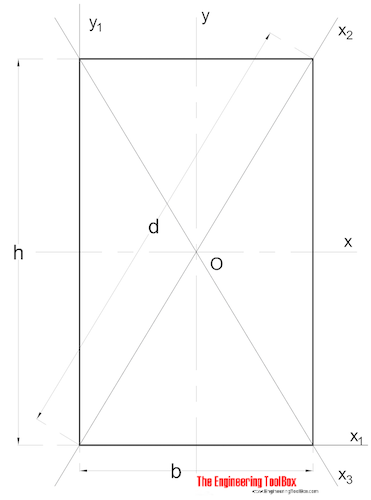
A Área de Momento de Ineria para uma secção rectangular pode ser calculado como

Ix = b h3 / 12 (3)

onde

b = largura

h = altura

Iy = b3 h / 12 (3b)

Sólida Secção Circular

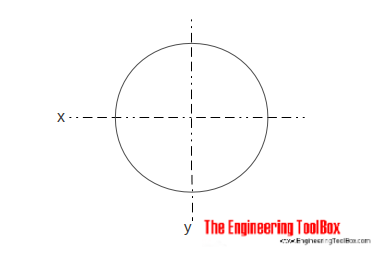
A Área de Momento de Inércia de um sólido cilíndrico de seção pode ser calculado como

Ix = π r4 / 4

= π d4 / 64 (4)

onde

r = raio

d = diâmetro

Iy = π r4 / 4

= π d4 / 64 (4b)

Oco Cilíndrico de Secção Transversal

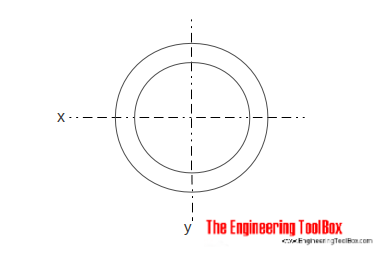
A Área de Momento de Inércia para uma cavidade cilíndrica de seção pode ser calculado como

Ix = π (do4 – di4) / 64 (5)

onde

do = cilindro de diâmetro exterior

di = cilindro de diâmetro interior

Iy = π (do4 – di4) / 64 (5b)

Seção Quadrada – Diagonal Momentos

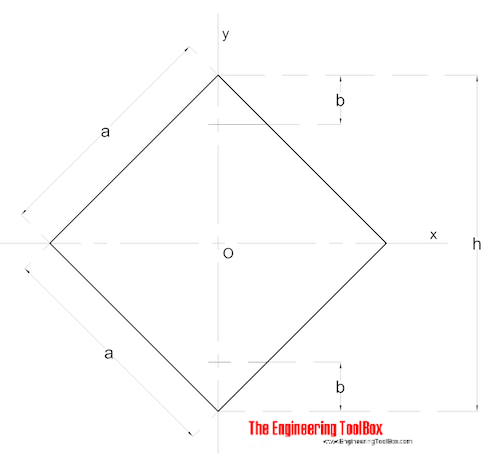
diagonal Área de Momentos de Inércia de uma seção quadrada pode ser calculado como

Ix = Iy = a4 / 12 (6)

Secção Rectangular – Área de Momentos em qualquer linha, através do Centro de Gravidade

secção Rectangular e Área de Momento em linha através do Centro de Gravidade pode ser calculado como

Ix = (b-h / 12) (h2 cos2 a + b2 sin2 um) (7)

a Forma Simétrica

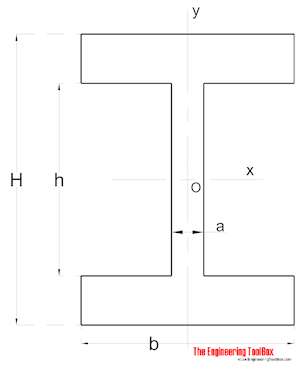
Área de Momento de Inércia para uma simétrica em forma de seção pode ser calculado como

Ix = (a h3 / 12) + (b / 12) (H3 – h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

Assimétrica Forma

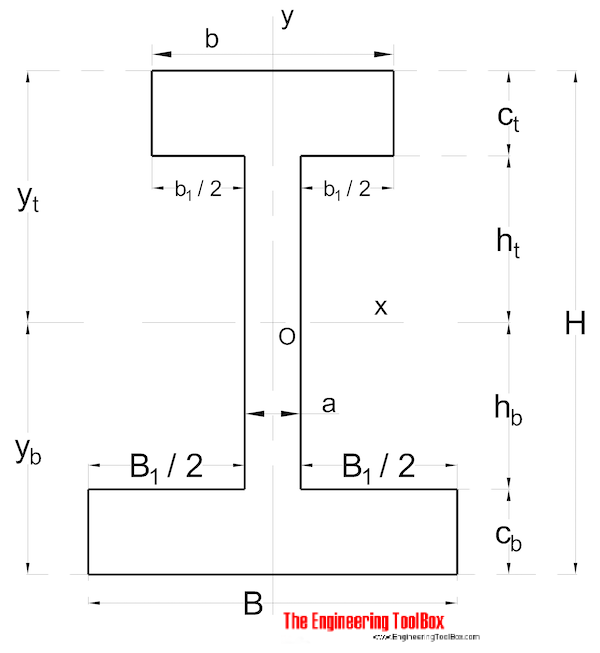
Área de Momento de Inércia para um não simétrica em forma de seção pode ser calculado como

Ix = (1 / 3) (B yb3 – B1 hb3 + b yt3 – b1 ht3) (9)

• Área de Momento de Inércia para uma típica Cruz Seções II

Área de Momento de Inércia vs. Momento Polar de Inércia vs. Momento de Inércia

• “Área de Momento de Inércia é uma propriedade de forma que é utilizada para calcular a deflexão, flexão e estresse em vigas
• “Momento Polar de Inércia” como uma medida de um feixe de capacidade para resistir à torção – o que é necessário para calcular a torção de uma viga submetida a torque
• “Momento de Inércia” é uma medida de um objeto é a resistência à mudança no sentido de rotação.

secção Módulo de elasticidade

• a “secção Módulo de elasticidade” é definida como W = I / y, em que I é o momento de inércia da área e y é a distância do eixo neutro a uma dada fibra