kde je funkce ve vysokém nebo nízkém bodě? Kalkul může pomoci!
maximální, je vysoká bodě a minimum, je nízký bod:
V plynule se měnící funkce maximální nebo minimální je vždy tam, kde funkce zplošťuje (s výjimkou pro sedlový bod).
kde se to zplošťuje? Kde je sklon nulový.
kde je sklon nula? Derivát nám to říká!
pojďme se ponořit přímo do příkladu:
- příklad: míč je hozen do vzduchu. Jeho výška kdykoli t je dána:
- jaká je jeho maximální výška?
- Rychlý Opakovací na Deriváty
- jak víme, že je to Maximum(nebo Minimum)?
- Druhá Derivace Test
- Příklad: Najít maxima a minima pro:
- Slova
- Ještě Jeden Příklad
- Příklad: Najít maxima a minima pro:
- musí být rozlišitelné
- příklad: a co funkce f (x) = |x / (absolutní hodnota)?
příklad: míč je hozen do vzduchu. Jeho výška kdykoli t je dána:
h = 3 + 14t-5t2
jaká je jeho maximální výška?
Pomocí derivátů můžeme najít sklon této funkce:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
(Viz níže příklad pro to, jak jsme zjistili, že derivát.)
Teď najít, když sklon je nulový:
sklon křivky je nulová v čase t = 1,4 sekundy
A výška na to, že čas je:
A tak:
maximální výška je 12,8 m (při t = 1.4 s)
Rychlý Opakovací na Deriváty
derivát v podstatě sklon funkce.
V předchozím příkladu jsme to:
h = 3 + 14t − 5t2
a přišel s tím derivace:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
Což nám říká, že sklon funkce v libovolném čase t
použili Jsme tyto Derivace Pravidla:
- Sklon konstantní hodnotu (3) je 0
- sklon přímky jako 2x 2, tak 14t má sklon 14
- funkce náměstí jako t2 má sklon 2t, tak 5t2 má sklon 5(2t)
- A pak jsme přidali je až: 0 + 14 − 5 (2 T)
jak víme, že je to Maximum(nebo Minimum)?
viděli jsme to na grafu! Ale jinak … deriváty přicházejí znovu na záchranu.
můžeme Vzít derivaci svahu (druhá derivace původní funkce):
Derivace 14 − 10t je -10
To znamená, že sklon je neustále zmenšuje (-10): cestování zleva doprava, sklon začíná pozitivní (funkci zvyšuje), prochází nulou (plochý bod), a pak sklon se stává negativní (funkce klesá):

sklon, který se zmenší (a jde i když 0), znamená maximum.
Toto se nazývá Druhá Derivace Test
Na výše uvedený graf ukázal jsem svahu před a po, ale v praxi jsme si udělat test na místě, kde svah je nula:
Druhá Derivace Test
Když funkce je sklon nulový v bodě x, a druhá derivace v x:
- menší než 0, jedná se o lokální maximum
- větší než 0, jedná se o lokální minimum
- se rovná 0, pak test selže (mohou existovat i jiné způsoby, jak zjistit, i když)
„Druhá Derivace: méně než 0, je maximální, větší než 0, je minimum“
Příklad: Najít maxima a minima pro:
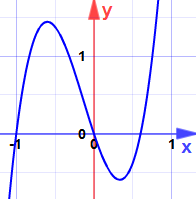
y = 5×3 + 2×2 − 3x
derivace (sklon) je:
![]() y = 15×2 + 4x− 3
y = 15×2 + 4x− 3
Což je kvadratická s nulami na:
- x = -3/5
- x = +1/3
mohou to být maxima nebo minima? (Ještě se nedívejte na graf!)
druhá derivace je y“ = 30x + 4
x = -3/5:
x = +1/3:
(Teď se můžete podívat na graf.)
Slova
vysoký bod se nazývá maximální (množné číslo maxima).
nízký bod se nazývá minimum (plurální minima).
obecné slovo pro maximum nebo minimum je extremum (plurální extrémy).
říkáme místní maximum (nebo minimum), když mohou být vyšší (nebo nižší) body jinde, ale ne poblíž.
Ještě Jeden Příklad
Příklad: Najít maxima a minima pro:
y = x3 − 6×2 + 12x − 5
derivace je:
![]() y = 3×2-12x + 12
y = 3×2-12x + 12
což je kvadratické s pouze jednou nulou na x = 2
je to maximum nebo minimum?
druhá derivace je y“ = 6x − 12
x = 2:
A tady je proč:
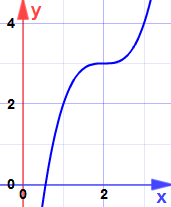
To je sedlový bod … sklon se stává nulovým, ale není ani maximem ani minimem.
musí být rozlišitelné
a je zde důležitý technický bod:
funkce musí být diferencovatelná (derivace musí existovat v každém bodě své domény).
příklad: a co funkce f (x) = |x / (absolutní hodnota)?
| |x| vypadá takto: |  |
V x=0 má velmi špičatý změnit!
ve skutečnosti tam není diferencovatelný (jak je znázorněno na diferencovatelné stránce).
takže tuto metodu nemůžeme použít pro funkci absolutní hodnoty.
funkce musí být také spojitá, ale každá funkce, která je diferencovatelná, je také spojitá, takže se nemusíte obávat.



