Oblast Moment Setrvačnosti – Typické průřezy

Oblast Moment Setrvačnosti nebo Moment Setrvačnosti Oblasti – známé také jako Druhý Moment Plochy – jsem, majetek tvar, který je použit k předpovědět deformace, ohýbání a napětí v nosnících.

Oblast Moment Setrvačnosti – Imperiální jednotky

• inches4

Oblast Moment Setrvačnosti – Metrické jednotky

• příponou mm4
• fond cm4
• m4

Převod mezi Jednotkami

• 1 fond cm4 = 10-8 m4 = 104 s příponou mm4
• 1 in4 = 4.16×105 příponou mm4 = 41.6 cm4

příklad-Převod mezi oblastním momentem setrvačných jednotek

9240 cm4 lze převést na mm4 vynásobením 104

(9240 cm4) 104 = 9.24 107 příponou mm4

Oblast Moment Setrvačnosti (Moment Setrvačnosti k určité Oblasti nebo Druhý Moment Plochy)

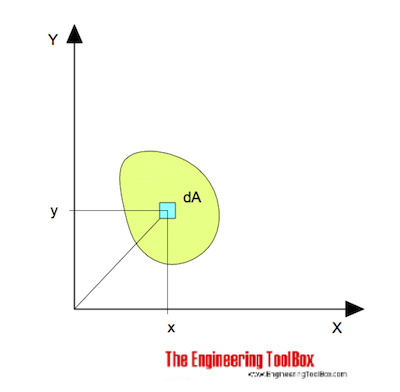
pro ohyb kolem osy x lze vyjádřit jako

Ix = ∫ y 2 dA (1)

, kde

Ix = Plocha Moment Setrvačnosti vztahující se k ose x (m4, s příponou mm4, inches4)

y = kolmá vzdálenost od osy x k prvku dA (m, mm, palce)

dA = elementární plocha (m2, mm2, inches2)

Moment Setrvačnosti pro ohýbání kolem osy y lze vyjádřit jako

Iy = ∫ x2 dA (2)

, kde

Iy = Plocha Moment Setrvačnosti vztahující se k ose y (m4, s příponou mm4, inches4)

x = kolmá vzdálenost od osy y k prvku dA (m, mm, palce)

Oblast Moment Setrvačnosti pro typické průřezy

• Oblast Moment Setrvačnosti pro typické průřezy II

Pevný Čtvercový průřez

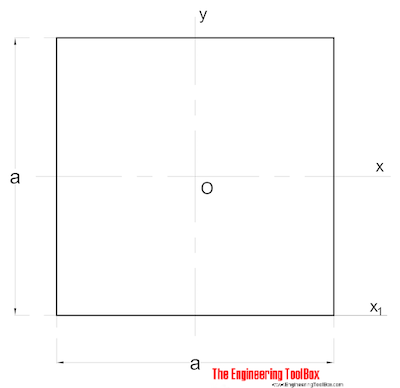
Oblast Moment Setrvačnosti pro pevné čtvercového průřezu lze vypočítat jako

Ix = a 4/ 12 (2)

kde

a = strana (mm, m, v..)

Iy = a4 / 12 (2b)

Pevný Obdélníkový průřez

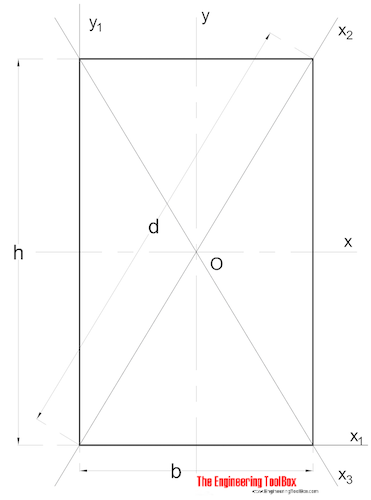
Oblast Okamžik Ineria pro obdélníkový řez může být vypočtena jako

Ix = b h3 / 12 (3)

kde

b = šířka

h = výška

Iy = b3, h / 12 (3b)

Pevný Kruhový průřez

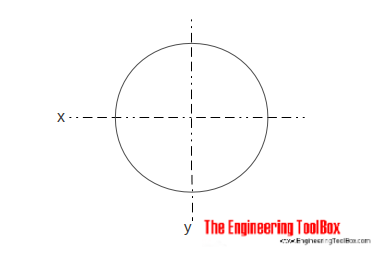
Oblast Moment Setrvačnosti pro pevné válcové části, může být vypočtena jako

Ix = π r4 / 4

= π d4 / 64 (4)

kde

r = poloměr

d = průměr

Iy = π r4 / 4

= π d4 / 64 (4b)

Dutého Válcového průřezu

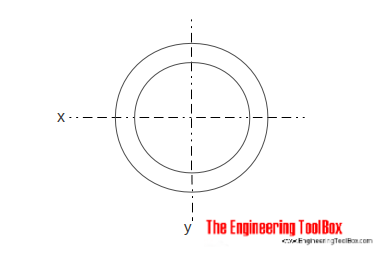
Oblast Moment Setrvačnosti pro dutý válcový oddíl může být vypočtena jako

Ix = π (do4 – di4) / 64 (5)

kde

= válec vnější průměr

di = vnitřní průměr válce

Iy = π (do4 – di4) / 64 (5b)

Čtvercového průřezu – Diagonální Okamžiky

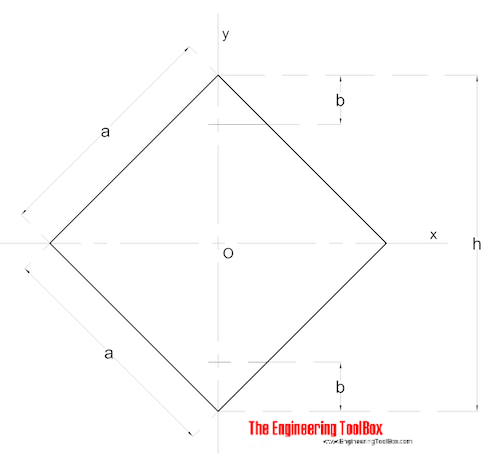
diagonální Plochy Momenty Setrvačnosti pro čtvercového průřezu lze vypočítat jako

Ix = Iy = a4 / 12 (6)

Obdélníkové Sekce – Oblast Okamžiky na všechny linky přes Centrum Gravitace

Obdélníkového průřezu a Plocha Chvíli on-line přes Těžiště lze vypočítat jako

Ix = (b, h / 12) (h2 cos2 a + b2 sin2 a) (7)

Symetrický Tvar

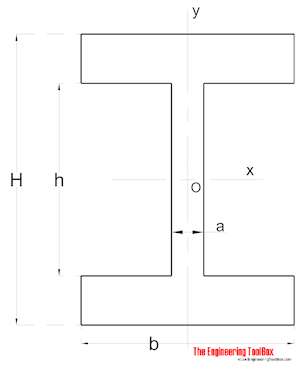
Oblast Moment Setrvačnosti pro symetrické ve tvaru oddíl může být vypočtena jako

Ix = (h3 / 12) + (b / 12) (H3 – h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

Nesymetrických Tvar

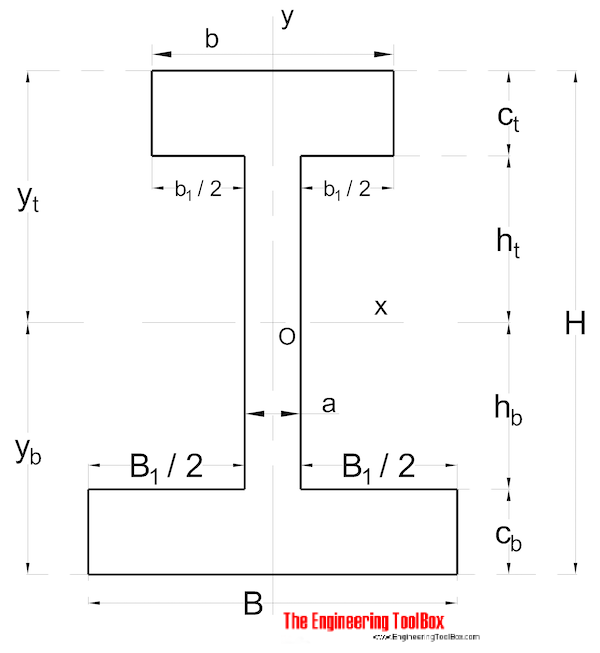
Oblast Moment Setrvačnosti pro non symetrické ve tvaru oddíl může být vypočtena jako

Ix = (1 / 3) (B yb3 – B1 hb3 + b yt3 – b1 ht3) (9)

• Oblast Moment Setrvačnosti pro typické průřezy II

Oblast Moment Setrvačnosti vs. Polární Moment Setrvačnosti vs. Moment Setrvačnosti

• „Oblast Moment Setrvačnosti“ je vlastnost tvar, který je použit k předpovědět deformace, ohýbání a napětí v nosnících
• „Polární Moment Setrvačnosti“ jako měřítko paprsek je schopnost odolávat kroucení – což je potřebné pro výpočet kroucení nosníku podroben momentu
• „Moment Setrvačnosti“ je měřítkem objektu je odpor ke změně ve směru otáčení.

Sekce Modul

• “ § Modul“ je definována jako W = I / y, kde I je Moment Setrvačnosti a y je vzdálenost od neutrální osy daného vlákna