Wenn unser Ziel darin besteht, die relativistische Verallgemeinerung der Poisson-Gleichung für das Gravitationsfeld zu finden:
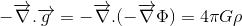
wo Φ sich auf das Gravitationspotential und ρ auf die Massendichte bezieht, sind wir auf halbem Weg.
Tatsächlich haben wir bereits in unserem vorherigen Artikel Der Energie-Impuls-Tensor gesehen, dass die Verallgemeinerung der Massendichte (rechter Term der Gleichung) dem Energie-Impuls Tµv entspricht.
Es erscheint daher vernünftig anzunehmen, dass unsere Gleichung die Form von:
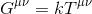
wobei k für einen Skalar und Gµv steht, stellt der Einstein-Tensor einen Rang-2-Tensor dar, der die Raumzeitkrümmung beschreibt .
Soweit wir wissen, sollte Gµv den folgenden Einschränkungen folgen:
– es sollte in flacher Raumzeit zunichte gemacht werden
– es sollte die Raumzeitkrümmung beschreiben und in Bezug auf den Riemann-Tensor linear sein
– es sollte symmetrisch sein und den Rang 2 haben (als Tµv)
– es sollte eine Nulldivergenz haben (als Tµv)
– und schließlich in Newton’scher 4nGp reduzieren
Erster Versuch mit Ricci-Tensor als Lösung
Wir erinnern uns aus unserem Artikel Die geodätische Gleichung in der Newtonschen Grenze, dass das Gravitationspotential Φ über h00=(g00-1)/c2 mit der 00-Komponente der Metrik verknüpft ist
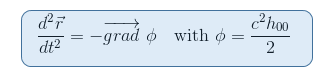
Es scheint dann natürlich, nach einem Tensor zu suchen, der die zweiten Ableitungen der Metrik beinhaltet, was für den Riemann-Tensor der Fall ist. Darüber hinaus ist der Riemann-Tensor der einzige Kandidat, den wir bisher kennen, um die Raumzeitkrümmung beschreiben zu können (vgl. zweite Einschränkung oben).
Da wir einen Rang-2-Tensor finden müssen, und wenn wir davon ausgehen, dass wir eine Lösung nur in Bezug auf den Riemann-Tensor finden müssen, scheint es natürlich, zuerst die kontrahierte Form des Riemann-Tensors zu betrachten, bekannt als der Ricci-Tensor.
Um dies zu sehen, erinnern wir uns an den Ausdruck des Riemann-Tensors aus dem Artikel Der Riemann-Krümmungstensor Teil II: Ableitung aus der geodätischen Abweichung
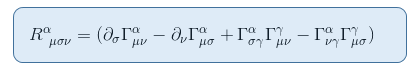
In der Grenze eines statischen und schwachen Gravitationsfeldes trägt nur ein Term zu R00 bei:
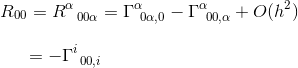
Im selben Artikel haben wir dieses Christoffel-Symbol berechnet und festgestellt, dass
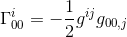
mit der Approximation von gij = nij und goo,j = hoo, j (siehe Artikel) erhalten wir:
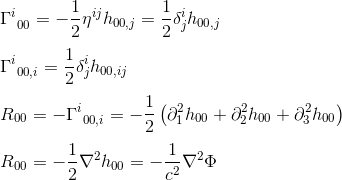
Die Identifizierung von R00 mit ΔΦ (Laplace-Operator) legt nahe, dass die Feldgleichung in der allgemeinen Relativitätstheorie Rab mit einem konstanten Vielfachen von Tab gleichsetzen sollte.
1915 war Einstein mit dieser Gleichung sogar in der Lage, das seit langem bestehende Problem der Merkurperihelpräzession zu lösen, was dazu führte, dass er im November desselben Jahres schrieb: „Für ein paar Tage war ich außer mir mit freudiger Aufregung.“
Schließlich musste Einstein diesen ersten Versuch ablehnen, da die Divergenz von Rab im Allgemeinen NICHT zunichte gemacht wird.
Zweiter Versuch
Es gibt einen Tensor, der eng mit dem Ricci-Skalar verwandt ist und ohne Widerspruch auf die linke Seite gestellt werden kann. Dies ergibt den Einstein-Tensor, der wie folgt definiert ist:
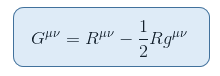
wobei R = Raa der Ricci-Skalar oder die Skalarkrümmung ist.
Diese Form von Gab ist symmetrisch und von Rang-2 und beschreibt offensichtlich die Raumzeitkrümmung. Es bleibt also nur zu zeigen, dass die Gesamtableitung Null ist
Dazu beginnen wir mit dem Die Bianchi-Identität
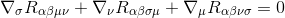
Multipliziert man mit gγσgαμgβν (die Metrikderivate sind Null, wirken also als Konstanten und können innerhalb der Derivate genommen werden), ergibt sich Folgendes:
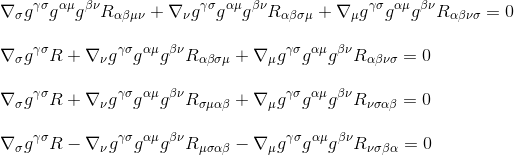
Durch Verwendung der Ricci-Tensordefinition Rµv = gμβgνσRβσ (Schritt 3) und durch Umbenennen der Indizes (Schritt 4) erhalten wir
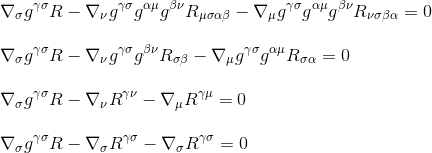
Durch Faktorisierung der Ableitung erhalten wir schließlich
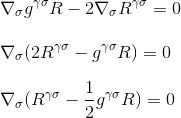
genau das wollten wir demonstrieren: Die Divergenz des Einstein-Tensors ist null, und wir haben den richtigen Kandidaten für die linke Seite unserer Krümmungs-Masse-Energie-Gleichung gefunden.