Flächenträgheitsmoment – Typische Querschnitte I

Flächenträgheitsmoment oder Trägheitsmoment für eine Fläche – auch bekannt als zweites Flächenträgheitsmoment – I, ist eine Eigenschaft der Form, die zur Vorhersage von Durchbiegung, Biegung und Spannung in Trägern verwendet wird.

Flächenträgheitsmoment – Imperiale Einheiten

• Zoll4

Flächenträgheitsmoment – Metrische Einheiten

• mm4
• cm4
• m4

Umrechnung zwischen Einheiten

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 zoll4 = 4,16 x 105 mm4 = 41.6 cm4

Beispiel – Umrechnung zwischen Flächenträgheitsmomenteinheiten

9240 cm4 kann durch Multiplikation mit 104

(9240 cm4) 104 = 9 in mm4 umgerechnet werden.24 107 mm4

Flächenträgheitsmoment (Trägheitsmoment für eine Fläche oder zweites Flächenmoment)

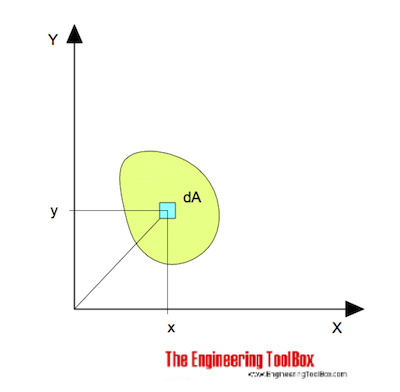
zum Biegen um die x-Achse kann ausgedrückt werden als

Ix = ∫ y2 dA (1)

wobei

Ix = Flächenträgheitsmoment bezogen auf die x-Achse (m4, mm4, Zoll4)

y = der senkrechte Abstand von der Achse x zum Element dA (m, mm, Zoll)

dA = eine elementare Fläche (m2, mm2, Zoll2)

Das Trägheitsmoment zum Biegen um die y-Achse kann ausgedrückt werden als

Iy = ∫ x2 dA (2)

wobei

Iy = Flächenträgheitsmoment bezogen auf die y-Achse (m4, mm4, Zoll4)

x = der senkrechte Abstand von der Achse y zum Element dA (m, mm, Zoll)

Flächenträgheitsmoment für typische Querschnitte I

• Flächenträgheitsmoment für typische Querschnitte II

Massiver quadratischer Querschnitt

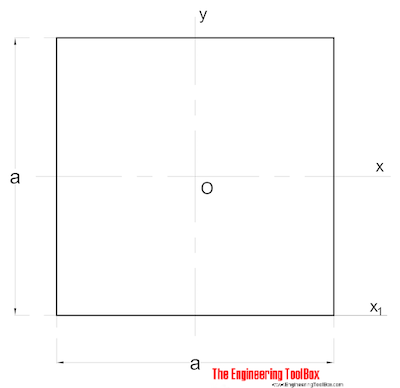
Das Flächenträgheitsmoment für einen massiven quadratischen Querschnitt kann berechnet werden als

Ix = a4 / 12 (2)

wobei

a = Seite (mm, m, in..)

Iy = a4 / 12 (2b)

Massiver rechteckiger Querschnitt

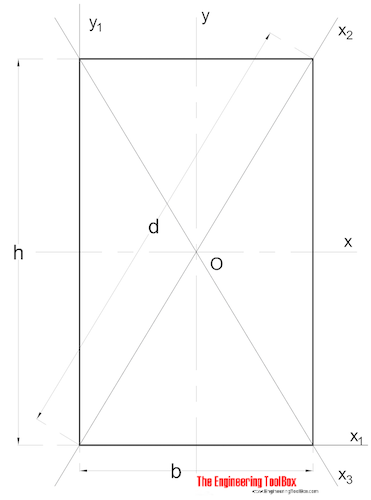
Das Flächenträgheitsmoment für einen rechteckigen Querschnitt kann berechnet werden als

Ix = b h3 / 12 (3)

wobei

b = Breite

h = Höhe

Iy = b3 h / 12 (3b)

Fester kreisförmiger Querschnitt

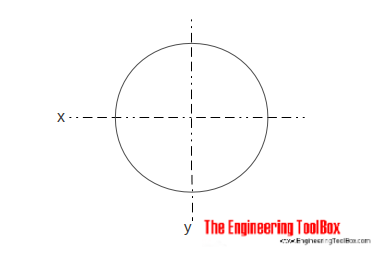
Das Flächenträgheitsmoment für einen festen zylindrischen Abschnitt kann berechnet werden als

Ix = π r4 / 4

= π d4 / 64 (4)

wobei

r = Radius

d = Durchmesser

Iy = π r4 / 4

= π d4 /64 (4b)

Hohlzylindrischer Querschnitt

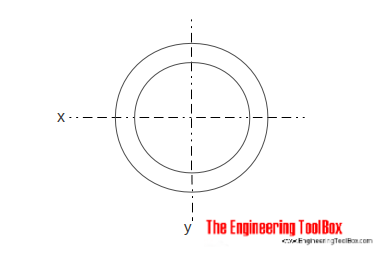
Das Flächenträgheitsmoment für einen hohlzylindrischen Abschnitt kann berechnet werden als

Ix = π (do4 – di4) / 64 (5)

wobei

do = Zylinderaußendurchmesser

di = Zylinderinnendurchmesser

Iy = π (do4 – di4) / 64 (5b)

Quadratischer Querschnitt – Diagonale Momente

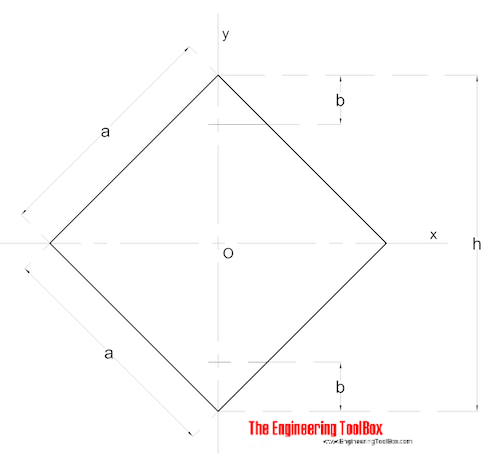
Die Trägheitsmomente der diagonalen Fläche für einen quadratischen Abschnitt können berechnet werden als

Ix = Iy = a4 / 12 (6)

Rechteckiger Querschnitt – Flächenmomente auf einer beliebigen Linie durch den Schwerpunkt

Rechteckiger Querschnitt und Momentenbereich auf einer Linie durch den Schwerpunkt können berechnet werden als

Ix = (b h / 12) (h2 cos2 a + b2 sin2 a) (7)

Symmetrische Form

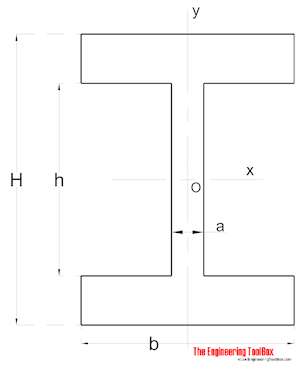
Flächenträgheitsmoment für a symmetrisch geformter Abschnitt kann berechnet werden als

Ix = (a h3 / 12) + (b / 12) (H3 – h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

Unsymmetrische Form

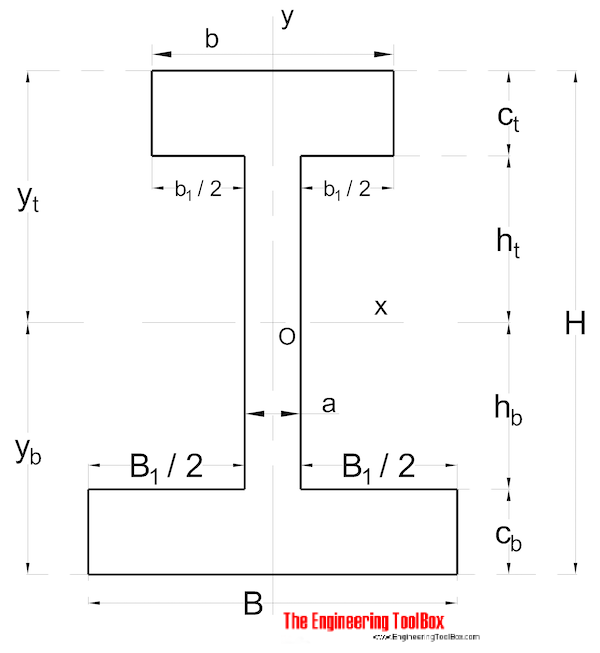
Flächenträgheitsmoment für einen nicht symmetrisch geformten Abschnitt kann berechnet werden als

Ix = (1 / 3) (B modell: yb3 – B1 hb3 + b yt3 – b1 ht3) (9)

• Flächenträgheitsmoment für typische Querschnitte II

Flächenträgheitsmoment vs. Polares Trägheitsmoment vs. Trägheitsmoment

• “ „Trägheitsmoment“ ist eine Eigenschaft der Form, die zur Vorhersage von Durchbiegung, Biegung und Spannung in Trägern verwendet wird
• „Polares Trägheitsmoment“ als Maß für die Fähigkeit eines Trägers, Torsion zu widerstehen – Dies ist erforderlich, um die Verdrehung eines Trägers zu berechnen, der einem Drehmoment ausgesetzt ist
• „Trägheitsmoment“ ist ein Maß für den Widerstand eines Objekts gegen eine Änderung der Drehrichtung.

Schnittmodul

• Der „Schnittmodul“ ist definiert als W = I / y, wobei I das Flächenträgheitsmoment und y der Abstand von der neutralen Achse zu einer beliebigen Faser ist