Si nuestro objetivo es encontrar la generalización relativista de la ecuación de Poisson para el campo gravitacional:
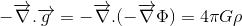
donde Φ se refiere al potencial gravitacional y ρ a la densidad de masa, estamos a mitad de camino.
De hecho, ya hemos visto en nuestro artículo anterior El tensor de energía-momento que la generalización de la densidad de masa (término de la mano derecha de la ecuación) corresponde al Tµv de energía-momento.
Parece razonable entonces asumir que nuestra ecuación debe tomar la forma de:
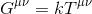
donde k representa un escalar y Gµv, llamado tensor de Einstein representa un tensor de rango 2 que describe la curvatura del espacio-tiempo .
Hasta donde sabemos, Gµv debe obedecer las siguientes restricciones:
– debe anularse en espacio – tiempo plano
– debe describir la curvatura del espacio – tiempo y ser lineal con respecto al tensor de Riemann
– debe ser simétrico y de rango 2 (como Tµv)
-debe tener una divergencia nula (como Tµv)
-y finalmente, en los límites newtonianos, debe reducirse a 4nGp
Primer intento con tensor de Ricci como solución
Recordamos de nuestro artículo La ecuación geodésica en el Límite Newtoniano que el potencial gravitacional Φ está vinculado al componente 00 de la métrica a través de h00=(g00-1)/c2
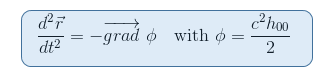
Parece entonces natural buscar un tensor que involucre las segundas derivadas de la métrica, que es el caso del tensor de Riemann. Además, el tensor de Riemann es el único candidato que conocemos hasta ahora para poder describir la curvatura del espacio-tiempo (véase la segunda restricción anterior).
Como tenemos que encontrar un tensor de rango 2, y si asumimos que tenemos que encontrar una solución únicamente en términos del tensor de Riemann, parece natural considerar primero la forma contraída del tensor de Riemann, conocido como tensor de Ricci.
Para ver esto, recordemos la expresión del tensor de Riemann del artículo The Riemann curvature tensor part II: derivación de la desviación geodésica
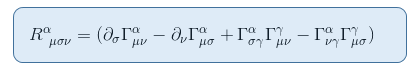
En el límite de un campo gravitacional estático y débil, solo un término contribuye a R00:
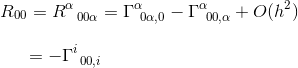
En el mismo artículo, hemos calculado este símbolo de Christoffel y encontramos que
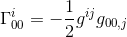
con la aproximación de gij = nij y goo, j = hoo, j (consulte el artículo) obtenemos:
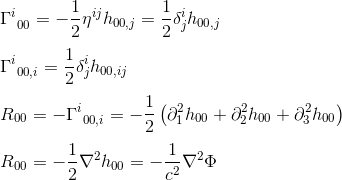
La identificación de R00 con ΔΦ (operador laplaciano) sugiere que la ecuación de campo en la relatividad general debe equiparar Rab a un múltiplo constante de Tab.
En 1915, usando esta ecuación, Einstein fue capaz incluso de resolver el problema de larga data de la precesión del perihelio de Mercurio, causando que escribiera en noviembre de ese año que, «Durante unos días, estaba fuera de mí con alegría.»
Eventualmente, Einstein tuvo que rechazar este primer intento, debido al hecho de que en general la divergencia de Rab NO anula.
Segundo intento
Hay un tensor estrechamente relacionado con el escalar Ricci que se puede colocar en el lado izquierdo sin contradicción. Esto da el tensor de Einstein definido de la siguiente manera:
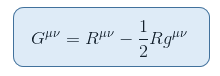
donde R = Raa es la curvatura escalar o escalar de Ricci.
Esta forma de Gab es simétrica y de rango 2 y obviamente describe la curvatura del espacio-tiempo. Así que solo queda mostrar que la derivada total es cero
Para hacer esto, comenzamos con la identidad Bianchi
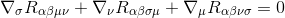
Multiplicando por gγσgαμgβν (las métricas derivadas son cero, por lo que actúan como constantes y se pueden tomar dentro de las derivadas), se obtiene:
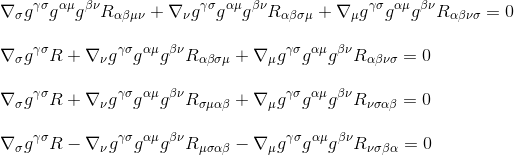
Usando la definición de tensor de Ricci Rµv = gμβgνσRβσ (paso 3) y renombrando los índices (paso 4), obtenemos
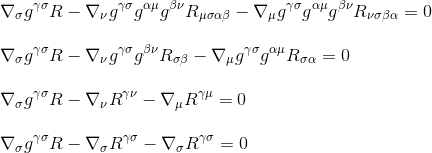
Al factorizar la derivada, finalmente obtenemos
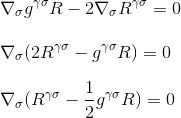
que es exactamente lo que queríamos demostrar: la divergencia del tensor de Einstein es nula, y hemos encontrado el candidato correcto para el lado izquierdo de nuestra ecuación de curvatura/masa-energía.