Rangos Intercuartílicos y Valores atípicos

• Púrpura
• MathHelp.com
• Encuentre los valores atípicos, si los hay, para el siguiente conjunto de datos:
• Encuentre los valores atípicos y extremos, si los hay, para el siguiente conjunto de datos y dibuje el gráfico de caja y bigote. Marque cualquier valor atípico con un asterisco y cualquier valor extremo con un punto abierto.

Púrpura

El «rango intercuartílico», abreviado» IQR», es solo el ancho de la caja en la gráfica de caja y bigote. Es decir, IQR = Q3-Q1 . El IQR se puede utilizar como una medida de la distribución de los valores.

Las estadísticas asumen que los valores están agrupados alrededor de algún valor central. El IQR indica la distribución de los valores «intermedios»; también se puede usar para decir cuándo algunos de los otros valores están «demasiado lejos» del valor central. Estos puntos » demasiado lejanos «se llaman» valores atípicos», porque» se encuentran fuera » del rango en el que los esperamos.

El IQR es la longitud de la caja en su gráfico de caja y bigote. Un valor atípico es cualquier valor que se encuentra más de una vez y media de la longitud de la caja desde cada extremo de la caja.

El Contenido Continúa A Continuación

MathHelp.com

Es decir, si un punto de datos está por debajo de Q1-1.5×IQR o por encima de Q3 + 1.5×IQR, se considera que está demasiado lejos de los valores centrales para ser razonable. Tal vez golpeaste la balanza cuando estabas haciendo esa medición, o tal vez tu compañero de laboratorio es un idiota y nunca deberías haberle dejado tocar ninguno de los equipos. Quién sabe? Pero cualquiera que sea su causa, los valores atípicos son aquellos puntos que no parecen «encajar».

Una vez que se sienta cómodo encontrando el IQR, puede pasar a localizar los valores atípicos, si los hay.

• Encuentre los valores atípicos, si los hay, para el siguiente conjunto de datos:

Los valores para Q1-1.5×IQR y Q3 + 1.5×IQR son las «vallas» que marcan los valores «razonables» de los valores atípicos. Los valores atípicos están fuera de las vallas.

Si su tarea le hace considerar no solo valores atípicos sino también «valores extremos», entonces los valores para Q1 – 1.5×IQR y Q3 + 1,5×IQR son las vallas » internas «y los valores para Q1 – 3×IQR y Q3 + 3×IQR son las vallas» externas».

Los valores atípicos (marcados con asteriscos o puntos abiertos) se encuentran entre las vallas interiores y exteriores, y los valores extremos (marcados con el símbolo que no usaste para los valores atípicos) están fuera de las vallas exteriores.

Por cierto, su libro puede referirse al valor de «1.5×IQR» como un «paso». Luego, los valores atípicos serán los números que están entre uno y dos pasos de las bisagras, y el valor extremo serán los números que están a más de dos pasos de las bisagras.

Mirando de nuevo el ejemplo anterior, las vallas exteriores estarían en 14.4-3×0.5 = 12.9 y 14.9 + 3×0.5 = 16.4. Dado que 16.4 está justo en la valla exterior superior, esto se consideraría solo un valor atípico, no un valor extremo. Pero 10.2 está completamente por debajo de la valla exterior inferior, por lo que 10.2 sería un valor extremo.

Su calculadora gráfica puede indicar o no si una gráfica de caja y bigote incluye valores atípicos. Por ejemplo, el problema anterior incluye los puntos 10.2, 15.9 y 16.4 como valores atípicos. Una configuración en mi calculadora gráfica proporciona el gráfico simple de caja y bigotes que utiliza solo el resumen de cinco números, por lo que los valores atípicos más lejanos se muestran como los puntos finales de los bigotes:

Una configuración de calculadora diferente proporciona la gráfica de caja y bigotes con los valores atípicos especialmente marcados (en este caso, con una simulación de un punto abierto), y los bigotes solo llegan hasta los valores más altos y más bajos que no son valores atípicos:

Mi calculadora no distingue entre valores atípicos y valores extremos. El tuyo tampoco. Revise su manual de instrucciones ahora, antes de la próxima prueba.

Si está utilizando su calculadora gráfica para ayudar con estas gráficas, asegúrese de saber qué configuración se supone que debe usar y qué significan los resultados, o la calculadora puede darle una respuesta perfectamente correcta pero «incorrecta».

• Encuentre los valores atípicos y extremos, si los hay, para el siguiente conjunto de datos y dibuje el gráfico de caja y bigote. Marque cualquier valor atípico con un asterisco y cualquier valor extremo con un punto abierto.

Advertisement

Para encontrar los valores atípicos y los valores extremos, primero tengo que encontrar el IQR. Ya hay siete valores en la lista, la mediana es el cuarto valor, por lo que:

Q2 = 25

La primera mitad de la lista es:

21, 23, 24

…de modo que T1 = 23; la segunda mitad es:

29, 33, 49

…así Q3 = 33. A continuación, el IQR se da por:

IQR = 33 – 23 = 10

Los valores atípicos serán los valores por debajo de:

23 – 1.5×10 = 23 – 15 = 8

…o por encima de:

33 + 1.5×10 = 33 + 15 = 48

Los valores extremos serán los que a continuación:

23 – 3×10 = 23 – 30 = -7

…o superior:

33 + 3×10 = 33 + 30 = 63

Así que tengo un valor atípico en 49, pero sin valores extremos. No tendré un bigote superior en mi parcela porque Q3 también es el valor no atípico más alto. Así que mi trama se ve así:

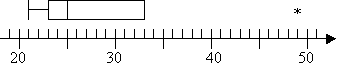
Cabe señalar que los métodos, términos y reglas descritos anteriormente son lo que he enseñado y lo que más comúnmente he visto enseñado. Sin embargo, su curso puede tener reglas específicas diferentes, o su calculadora puede hacer cálculos ligeramente diferentes. Es posible que deba ser algo flexible para encontrar las respuestas específicas de su currículo.