Maksimien ja minimien löytäminen Derivaatoilla

esimerkki: pallo heitetään ilmaan. Sen korkeus millä hetkellä tahansa t on:

h = 3 + 14t-5t2

mikä on sen suurin korkeus?

derivaatoilla voidaan löytää kyseisen funktion kulmakerroin:

h = 0 + 14 − 5 (2t)
= 14 − 10t

(Katso tämän esimerkin alta, miten löysimme kyseisen derivaatan.)

nyt löydetään, kun kaltevuus on nolla:

kaltevuus on nolla t = 1,4 sekuntia

ja korkeus on tuolloin:

ja niin:

suurin korkeus on 12,8 m (at t = 1,4 s)

nopea kertaus Derivaatoille

derivaatta löytää periaatteessa funktion kaltevuuden.

edellisessä esimerkissä otimme tämän:

h = 3 + 14t-5t2

ja keksimme tämän derivaatan:

h = 0 + 14 − 5(2t)
= 14-10t

joka kertoo funktion kaltevuuden milloin tahansa t

käytimme näitä Johdannaissääntöjä:

• vakion arvon (kuten 3) kaltevuus on 0
• suoran kuten 2x kaltevuus on 2, joten 14T: n kaltevuus on 14
• neliöfunktion kuten t2 kaltevuus on 2t, joten 5t2: n kaltevuus on 5(2t)
• ja sitten laskimme ne ylös: 0 + 14 − 5 (2t)

tätä kutsutaan toiseksi Derivaattakokeeksi

toinen Derivaattakoe

kun funktion kulmakerroin on nolla pisteessä x ja toinen derivaatta pisteessä x on:

• alle 0, se on paikallinen maksimi
• suurempi kuin 0, se on paikallinen minimi
• yhtä suuri kuin 0, sitten testi epäonnistuu (voi olla muitakin tapoja selvittää)

esimerkki: Etsi maksimit ja minimit:

y = 5×3 + 2×2-3x

derivaatta (kaltevuus) on:

y = 15×2 + 4x− 3

joka on quadratic kanssa nollia at:

• x = -3/5
• x = +1/3

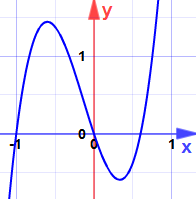
voisivatko ne olla maksimeja tai minimejä? (Älä katso graafia vielä!)

toinen derivaatta on y” = 30x + 4

At x = -3/5:

At x = +1/3:

(nyt voit katsoa kuvaajaa.)

korkeaa pistettä kutsutaan maksimiksi (monikossa maksimiksi).

alinta pistettä kutsutaan minimiksi (monikkominimiksi).

maksimia tai minimiä tarkoittava yleissana on extremum (monikossa extrema).

sanomme paikalliset maksimit (tai minimit), kun muualla voi olla korkeampia (tai matalampia) pisteitä, mutta ei lähellä.

esimerkki: Etsi maksimit ja minimit:

y = x3-6×2 + 12x-5

derivaatta on:

y = 3×2 − 12x + 12

joka on neliö, jossa on vain yksi nolla pisteessä x = 2

onko se maksimi vai minimi?

toinen derivaatta on y” = 6x − 12

At x = 2:

ja tässä syy:

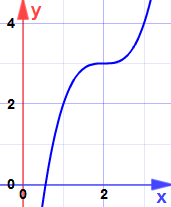
se on satulapiste … rinteestä tulee kyllä nolla, mutta se ei ole maksimi eikä minimi.

esimerkki: entä funktio f(x) = |x| (itseisarvo) ?

|X / näyttää tältä:

At x=0 se on hyvin terävä muutos!

itse asiassa se ei ole differentioitavissa siellä (kuten differentiable-sivulla näkyy).

joten tätä menetelmää ei voi käyttää itseisarvofunktiolle.