Moment d’Inertie de l’Aire – Sections Transversales typiques I

Moment d’Inertie de l’Aire ou Moment d’Inertie pour une Aire – également appelée Deuxième Moment de l’Aire-I, est une propriété de forme utilisée pour prédire la déflexion, la flexion et la contrainte dans les poutres.

Moment d’Inertie de Surface – Unités impériales

• pouces4

Moment d’Inertie de Surface – Unités métriques

• mm4
• cm4
• m4

Conversion entre unités

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 po4 = 4.16×105 mm4 = 41.6 cm4

Exemple de conversion entre les Unités de Moment d’inertie de surface

9240 cm4 peut être converti en mm4 en multipliant par 104

(9240 cm4) 104 = 9.24 107 mm4

Moment d’Inertie de l’Aire (Moment d’Inertie pour une Aire ou Second Moment de l’Aire)

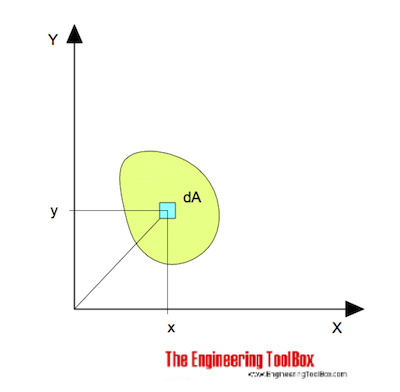
pour la flexion autour de l’axe x peut être exprimé comme

Ix = ∫y2 dA(1)

où

Ix = Moment d’Inertie d’Aire lié à l’axe x (m4, mm4, pouces 4)

y = la distance perpendiculaire de l’axe x à l’élément dA (m, mm, pouces)

dA = une surface élémentaire (m2, mm2, pouces2)

Le moment d’inertie pour la flexion autour de l’axe y peut être exprimé en

Iy = ∫x2 dA(2)

où

Iy = Moment d’Inertie de l’aire lié à l’axe y (m4, mm4, pouces 4)

x = la distance perpendiculaire de l’axe y à l’élément dA (m, mm, pouces)

Moment d’Inertie de l’aire pour des sections transversales typiques I

• Moment d’Inertie de l’Aire pour les Sections transversales typiques II

Section Carrée Pleine

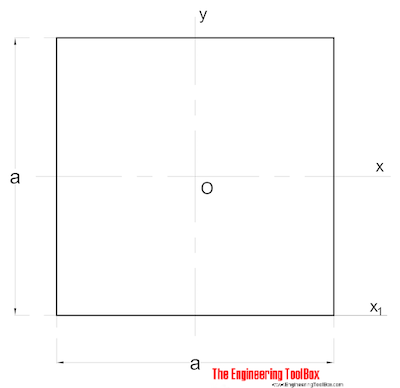
Le Moment d’Inertie de l’Aire pour une section carrée pleine peut être calculé comme

Ix = a4 / 12 (2)

où

a = côté (mm, m, in..)

Iy = a4/12 (2b)

Section Transversale Rectangulaire Pleine

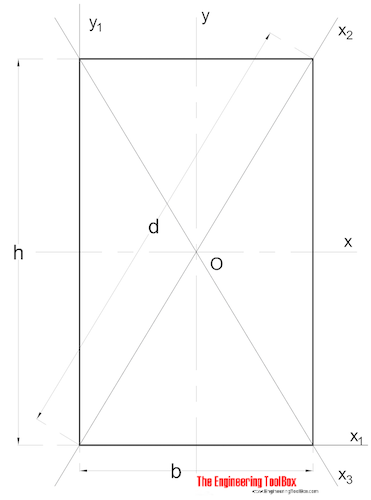
Le Moment de l’aire d’Ineria pour une section rectangulaire peut être calculé comme

Ix = b h3 / 12 (3)

où

b = largeur

h = hauteur

Iy = b3 h/12 (3b)

Section Circulaire pleine

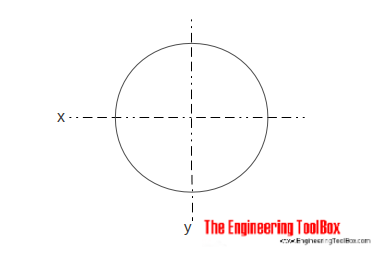
Le Moment d’Inertie de l’Aire pour une section cylindrique pleine peut être calculé comme

Ix = π r4/4

= π d4 / 64 (4)

où

r = rayon

d = diamètre

Iy = π r4/4

= π d4/64 (4b)

Section Cylindrique creuse

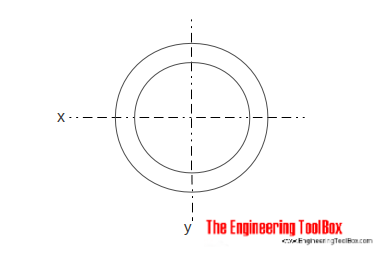
Le Moment d’Inertie de l’Aire pour une section cylindrique creuse peut être calculé comme

Ix = π(do4-di4) / 64 (5)

où

do = diamètre extérieur du cylindre

di = diamètre intérieur du cylindre

Iy = π(do4-di4) / 64(5b)

Section carrée – Moments Diagonaux

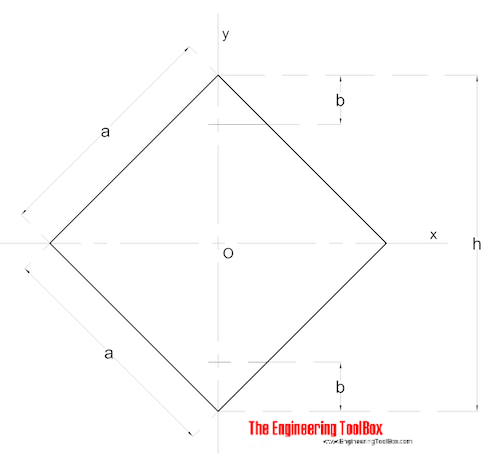
Les Moments d’Inertie d’aire diagonale pour une section carrée peuvent être calculés comme

Ix= Iy=a4 / 12 (6)

Section rectangulaire – Moments d’Aire sur n’importe quelle ligne passant par le Centre de gravité

La section rectangulaire et l’Aire de Moment sur la ligne passant par le Centre de Gravité peuvent être calculées comme

Ix =(b h/12) (h2 cos2 a + b2 sin2 a) (7)

Forme symétrique

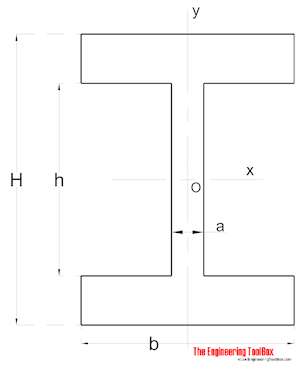
Moment d’Inertie de l’Aire pour a la section de forme symétrique peut être calculée comme

Ix = (a h3/12) + (b/12) (H3-h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H-h) (8b)

Forme non symétrique

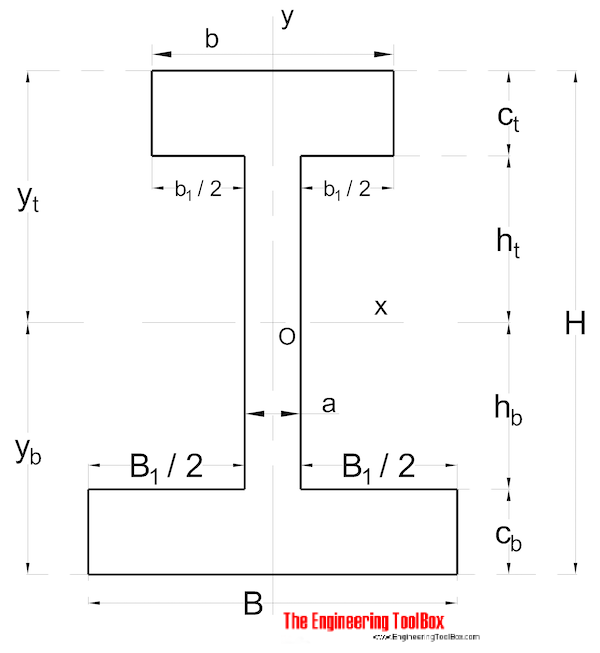
Le Moment d’inertie de l’aire pour une section de forme non symétrique peut être calculé comme

Ix = (1 / 3) (B yb3-B1 hb3 +b yt3-b1 ht3) (9)

• Moment d’Inertie de l’Aire pour les Sections transversales typiques II

Moment d’Inertie de l’Aire par rapport au Moment d’Inertie Polaire par rapport au Moment d’Inertie polaire. Moment d’Inertie

•  » Le « Moment d’inertie de l’aire » est une propriété de forme utilisée pour prédire la déflexion, la flexion et la contrainte dans les poutres
• « Moment d’inertie polaire » en tant que mesure de la capacité d’un faisceau à résister à la torsion – ce qui est nécessaire pour calculer la torsion d’un faisceau soumis à un couple
• « Moment d’inertie » est une mesure de la résistance d’un objet au changement de sens de rotation.

Module de section

• le « Module de section » est défini comme W = I/y, où I est le Moment d’Inertie de l’aire et y est la distance entre l’axe neutre et une fibre donnée