Terület Tehetetlenségi nyomaték-tipikus keresztmetszetek i

terület Tehetetlenségi nyomaték vagy Tehetetlenségi nyomaték egy területre – más néven a terület második nyomatéka-I, olyan alakzat tulajdonsága, amelyet a gerendák elhajlásának, hajlításának és feszültségének előrejelzésére használnak.

terület Tehetetlenségi nyomaték – birodalmi egységek

• hüvelyk4

terület Tehetetlenségi nyomaték – metrikus egységek

• mm4
• cm4
• m4

átváltás egységek között

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4, 16×105 mm4 = 41.6 cm4

példa – Konvertálás a terület között Tehetetlenségi nyomaték egységek

9240 cm4 átalakítható mm4-re a 104

(9240 cm4) 104 = 9 szorzatával.24 107 mm4

terület tehetetlenségi nyomatéka (egy területre vonatkozó Tehetetlenségi nyomaték vagy a terület második nyomatéka)

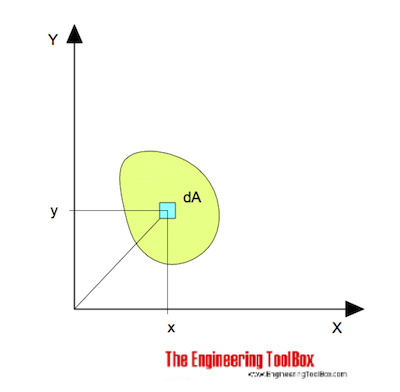
kifejezhető

IX = 6-2 da (1)

ahol

Ix = az x tengelyhez kapcsolódó Tehetetlenségi nyomaték (m4, mm4, hüvelyk4)

y = az X tengelyre merőleges az X tengelytől a Da elemig (m, mm, hüvelyk)

dA = elemi terület (m2, mm2, hüvelyk2)

a hajlítás tehetetlenségi nyomatéka az y tengely körül kifejezhető:

Iy = 6×2 da (2)

ahol

Iy = az y tengelyhez kapcsolódó Tehetetlenségi nyomaték (m4, mm4, hüvelyk4)

x = az y tengelytől a dA elemig (m, mm, hüvelyk) merőleges távolság

terület tehetetlenségi nyomatéka tipikus Keresztmetszeteknél I

• terület tehetetlenségi nyomaték a tipikus II keresztmetszetekhez

szilárd négyzet keresztmetszet

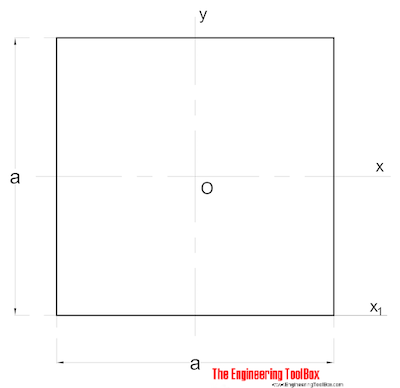
a terület tehetetlenségi nyomatéka egy szilárd négyzet keresztmetszethez a következőképpen számítható ki:

IX = a4 / 12 (2)

ahol

A = oldal (mm, m, ban ben..)

Iy = A4 / 12 (2B)

Tömör téglalap keresztmetszet

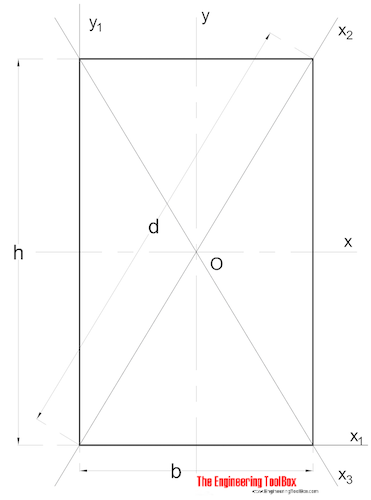
az Ineria Területnyomatéka egy téglalap alakú szakasz esetében a következőképpen számítható ki:

Ix = b h3 / 12 (3)

ahol

b = szélesség

h = magasság

Iy = b3 h / 12 (3B)

szilárd kör keresztmetszet

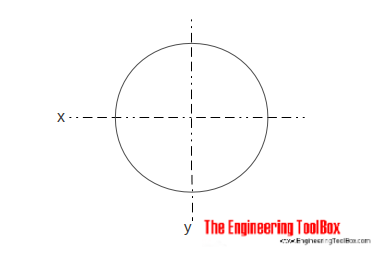
a terület tehetetlenségi nyomatéka egy szilárd hengeres keresztmetszet esetében a következőképpen számítható ki:

Ix = ons r4 / 4

= D4 ons / 64 (4)

ahol

r = sugár

d = átmérő

IY = xhamstergömb r4 / 4

= D4 / 64 (4B)

üreges hengeres keresztmetszet

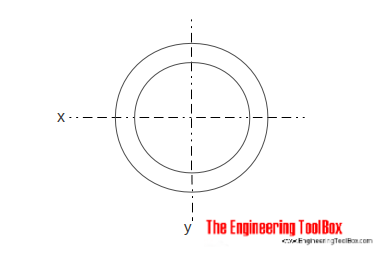
az üreges hengeres keresztmetszethez tartozó Tehetetlenségi nyomaték a következőképpen számítható ki:

Ix = ons (do4-di4) / 64 (5)

ahol

do = henger külső átmérője

di = henger belső átmérője

IY = (DO4 – di4) / 64 (5b)

négyzet alakú szakasz – Átlós momentumok

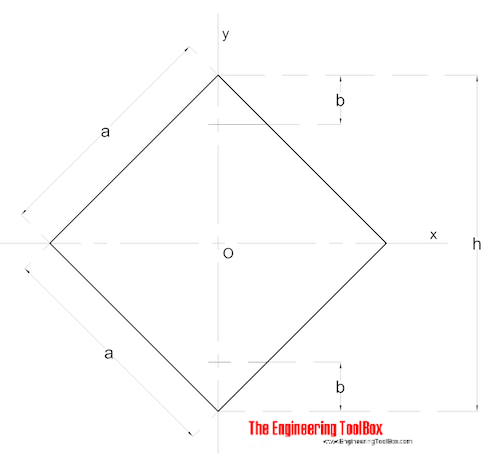
az átlós terület tehetetlenségi momentumai egy négyzetszakasz esetében a következőképpen számíthatók ki:

Ix = Iy = a4 / 12 (6)

négyszögletes szakasz-terület pillanat bármely vonalon keresztül súlypont

a négyszögletes szakasz és a pillanat területe a vonalon keresztül súlypont kiszámítható

Ix = (b h / 12) (h2 cos2 a + b2 sin2 a) (7)

szimmetrikus alak

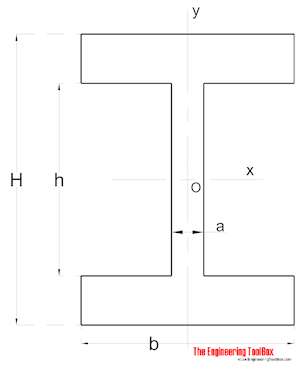
terület Tehetetlenségi nyomaték a szimmetrikus alakú szakasz lehet kiszámítani, mint

Ix = (a h3 / 12) + (b / 12) (H3 – h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

nem szimmetrikus alak

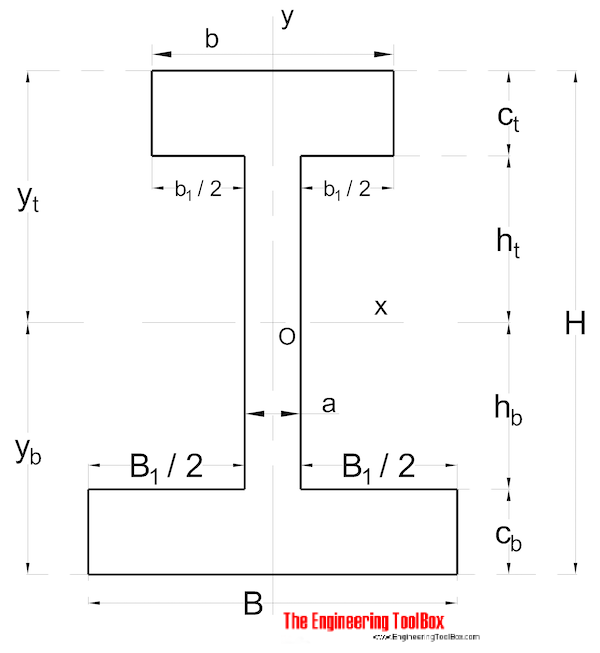
terület Tehetetlenségi nyomaték egy nem szimmetrikus alakú szakaszra a következőképpen számítható ki:

Ix = (1 / 3) (B Yb3 – B1 HB3 + B YT3 – B1 HT3) (9)

• terület tehetetlenségi nyomatéka a tipikus II Keresztmetszeteknél

terület tehetetlenségi nyomatéka vs. poláris Tehetetlenségi nyomaték vs. Tehetetlenségi nyomaték

• “terület Tehetetlenségi nyomaték”olyan alakzat, amelyet a gerendák alakváltozásának, hajlításának és feszültségének előrejelzésére használnak
• ” poláris Tehetetlenségi nyomaték”a gerenda torziós ellenállási képességének mércéjeként – amely a nyomatéknak kitett gerenda csavarodásának kiszámításához szükséges
• ” Tehetetlenségi nyomaték ” az objektum Forgásirány-változással szembeni ellenállásának mértéke.

szakasz Modulus

• a “szakasz Modulus” meghatározása: W = I / y, ahol I a terület tehetetlenségi nyomatéka, y pedig a semleges tengelytől az adott szálig terjedő távolság