Come si segnala una correlazione di Spearman?
Il modo in cui si segnala il coefficiente di correlazione di uno Spearman dipende dal fatto che sia stata determinata o meno la significatività statistica del coefficiente. Se hai semplicemente eseguito la correlazione Spearman senza alcun test di significatività statistica, sei in grado di indicare semplicemente il valore del coefficiente come mostrato di seguito:
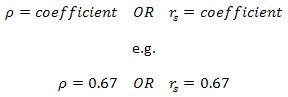
Tuttavia, se sono stati eseguiti anche test di significatività statistica, è necessario includere ulteriori informazioni come mostrato di seguito:
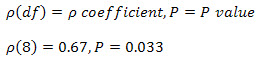
dove df = N – 2, dove N = numero di casi a coppie.
Come si esprime l’ipotesi nulla per questo test?
La forma generale di un’ipotesi nulla per una correlazione di Spearman è:
H0: Non esiste alcuna associazione tra le due variabili .
Ricorda, stai facendo un’inferenza dal tuo campione alla popolazione che il campione dovrebbe rappresentare. Tuttavia, poiché questa è una comprensione generale di un test statistico inferenziale, spesso non è inclusa. Una dichiarazione di ipotesi nulla per l’esempio usato in precedenza in questa guida sarebbe:
H0: Non esiste alcuna associazione tra matematica e segni inglesi.
Come posso interpretare una correlazione di Spearman statisticamente significativa?
È importante rendersi conto che la significatività statistica non indica la forza della correlazione di Spearman. Infatti, il test di significatività statistica della correlazione Spearman non fornisce alcuna informazione sulla forza della relazione. Pertanto, il raggiungimento di un valore di p = 0,001, ad esempio, non significa che la relazione sia più forte di se si ottiene un valore di p = 0,04. Questo perché il test di significatività sta indagando se è possibile rifiutare o non riuscire a rifiutare l’ipotesi nulla. Se si imposta α = 0.05, il raggiungimento di una correlazione statisticamente significativa Spearman rank-order significa che puoi essere sicuro che c’è meno di un 5% di possibilità che la forza della relazione che hai trovato (il tuo coefficiente ρ) sia avvenuta per caso se l’ipotesi nulla fosse vera.