Se il nostro obiettivo è quello di trovare la generalizzazione relativistica di Poisson ‘s equazione per il campo gravitazionale:
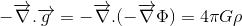
dove Φ si riferisce al potenziale gravitazionale e ρ per la densità di massa, siamo a metà strada.
In effetti, abbiamo già visto nel nostro precedente articolo Il tensore energia-momento che la generalizzazione della densità di massa (termine destro dell’equazione) corrisponde al Tµv energia-momento.
Sembra quindi ragionevole supporre che la nostra equazione dovrebbe assumere la forma di:
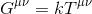
dove k sta per uno scalare e Gµv, chiamato il tensore di Einstein rappresenta un tensore rank-2 che descrive la curvatura dello spaziotempo .
Per quanto ne sappiamo, Gµv dovrebbe rispettare i seguenti vincoli:
– dovrebbe annullare in tv spaziotempo
– dovrebbe descrivere la curvatura dello spazio-tempo e lineare rispetto al tensore di Riemann
– deve essere simmetrica e di rango 2 (come Tµv)
– dovrebbe avere un valore null divergenza (come Tµv)
– e, infine, in Newtoniana limiti, si dovrebbe ridurre a 4nGp
Primo tentativo con tensore di Ricci come soluzione
ricordiamo che dal nostro articolo Geodetiche equazione Newtoniana Limite che il potenziale gravitazionale Φ è legata alle 00-componente della metrica via h00=(g00-1)/c2
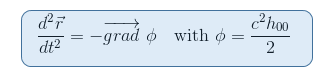
Sembra quindi naturale cercare un tensore che coinvolga le seconde derivate della metrica, che è il caso del tensore di Riemann. Inoltre, il tensore di Riemann è l’unico candidato che conosciamo finora per essere in grado di descrivere la curvatura dello spaziotempo (cfr.secondo vincolo sopra).
Poiché dobbiamo trovare un tensore di rango 2, e se assumiamo che dobbiamo trovare una soluzione esclusivamente in termini di tensore di Riemann, sembra naturale considerare prima la forma contratta del tensore di Riemann, noto come tensore di Ricci.
Per vedere questo, ricordiamo l’espressione del tensore di Riemann da tha articolo Il tensore di curvatura di Riemann parte II: derivazione dalla deviazione geodetica
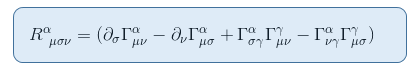
Nel limite di statica e di un debole campo gravitazionale, con un solo termine contribuisce a R00:
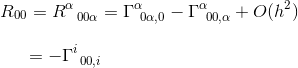
Nello stesso articolo, abbiamo calcolato questo simbolo di Christoffel e ha scoperto che
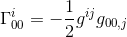
con l’approssimazione di gij = nij e goo,j = hoo,j (vedi articolo) si ottiene:
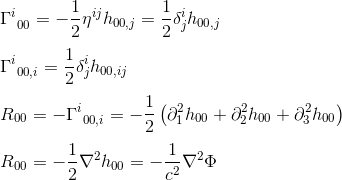
L’identificazione di R00 con ΔΦ (operatore laplaciano) suggerisce che l’equazione di campo nella relatività generale dovrebbe equiparare Rab a un multiplo costante di Tab.
Nel 1915, usando questa equazione, Einstein fu persino in grado di risolvere il problema di lunga data della precessione del perielio di Mercurio, facendo scrivere nel novembre di quell’anno che, “Per alcuni giorni, ero fuori di me con gioiosa eccitazione.”
Alla fine, Einstein ha dovuto rifiutare questo primo tentativo, a causa del fatto che in generale la divergenza di Rab NON annulla.
Secondo tentativo
C’è un tensore strettamente correlato allo scalare di Ricci che può essere messo sul lato sinistro senza contraddizione. Questo dà il tensore di Einstein definito come segue:
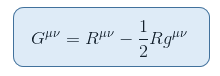
dove R = Raa è la curvatura scalare di Ricci o scalare.
Questa forma di Gab è simmetrica e di rango-2 e ovviamente descrive la curvatura dello spaziotempo. Quindi resta solo da dimostrare che la derivata totale è zero
Per fare ciò, iniziamo con l’identità Bianchi
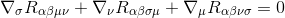
Moltiplicando per gγσgαμgβν (le derivate metriche sono zero, quindi agiscono come costanti e possono essere prese all’interno delle derivate), si ottiene:
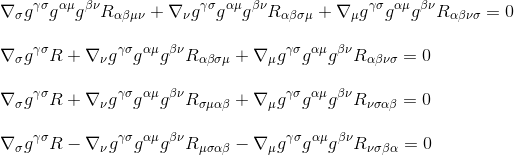
utilizzando il tensore di Ricci definizione Rµv=gμβgνσRβσ (passo 3) e rinominando gli indici (passo 4), otteniamo
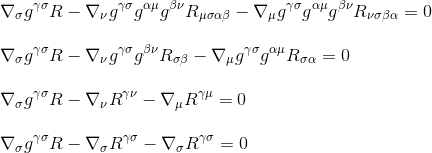
Da factorising derivati, abbiamo finalmente ottenere
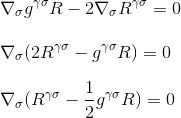
che è esattamente quello che volevamo dimostrare: la divergenza del tensore di Einstein è null, e abbiamo trovato il giusto candidato per la sinistra del nostro curvatura/equazione massa-energia.