Interquartile Ranges & Outliers

• Purplemath
• MathHelp.com
• Trova i valori anomali, se presenti, per il seguente set di dati:
• Trova i valori anomali e i valori estremi, se presenti, per il seguente set di dati e disegna il grafico box-and-whisker. Segna eventuali valori anomali con un asterisco e qualsiasi valore estremo con un punto aperto.

Purplemath

La “gamma interquartile”, abbreviata “IQR”, è solo la larghezza della scatola nella trama box-and-whisker. Cioè, IQR = Q3-Q1 . L’IQR può essere utilizzato come misura di come spread-out i valori sono.

Le statistiche presuppongono che i valori siano raggruppati attorno a un valore centrale. L’IQR indica come sono distribuiti i valori “medi”; può anche essere usato per dire quando alcuni degli altri valori sono “troppo lontani” dal valore centrale. Questi punti ” troppo lontani “sono chiamati” valori anomali”, perché” si trovano al di fuori ” dell’intervallo in cui li aspettiamo.

L’IQR è la lunghezza della scatola nella trama box-and-whisker. Un outlier è qualsiasi valore che si trova più di una volta e mezza la lunghezza della casella da entrambe le estremità della casella.

Il contenuto continua qui sotto

MathHelp.com

Cioè, se un punto dati è inferiore a Q1-1,5×IQR o superiore a Q3 + 1,5×IQR, è considerato troppo lontano dai valori centrali per essere ragionevole. Forse hai urtato la bilancia quando stavi facendo quella misura, o forse il tuo compagno di laboratorio è un idiota e non avresti mai dovuto lasciarlo toccare nessuna delle apparecchiature. Chi lo sa? Ma qualunque sia la loro causa, i valori anomali sono quei punti che non sembrano “adattarsi”.

Una volta che sei a tuo agio nel trovare l’IQR, puoi passare alla localizzazione dei valori anomali, se presenti.

• Trova i valori anomali, se presenti, per il seguente set di dati:

I valori per il Q1 – 1.5×IQR e Q3 + 1.5×IQR sono i “recinti” che delimitano il “ragionevole” i valori i valori outlier. Valori anomali si trovano al di fuori delle recinzioni.

Se il tuo incarico sta considerando non solo valori anomali ma anche” valori estremi”, allora i valori per Q1 – 1.5×IQR e Q3 + 1.5×IQR sono i recinti “interni” ed i valori per Q1-3×IQR e Q3 + 3×IQR sono i recinti “esterni”.

I valori anomali (contrassegnati con asterischi o punti aperti) si trovano tra le recinzioni interne ed esterne e i valori estremi (contrassegnati con qualsiasi simbolo non utilizzato per i valori anomali) si trovano al di fuori delle recinzioni esterne.

A proposito, il tuo libro potrebbe riferirsi al valore di “1.5×IQR” come a un “passo”. Quindi i valori anomali saranno i numeri che si trovano tra uno e due passi dalle cerniere, e il valore estremo saranno i numeri che sono più di due passi dalle cerniere.

Guardando di nuovo l’esempio precedente, le recinzioni esterne sarebbero a 14,4 – 3×0,5 = 12,9 e 14,9 + 3×0,5 = 16,4. Poiché 16.4 è proprio sulla recinzione esterna superiore, questo sarebbe considerato solo un valore anomalo, non un valore estremo. Ma 10.2 è completamente al di sotto della recinzione esterna inferiore, quindi 10.2 sarebbe un valore estremo.

La calcolatrice grafica può o non può indicare se una trama box-and-whisker include valori anomali. Ad esempio, il problema di cui sopra include i punti 10.2, 15.9 e 16.4 come valori anomali. Un’impostazione sul mio calcolatore grafico fornisce la semplice trama box-and-whisker che utilizza solo il riepilogo a cinque numeri, quindi i valori anomali più lontani sono mostrati come gli endpoint dei baffi:

Un’altra calcolatrice consente di impostare la box-and-whisker plot con gli outliers appositamente contrassegnati (in questo caso, con una simulazione di un open dot), e i baffi di andare solo per quanto riguarda i valori massimi e minimi che non sono valori anomali:

la Mia calcolatrice non fa alcuna distinzione tra valori anomali e valori estremi. Il tuo non può, neanche. Controlla il manuale del tuo proprietario ora, prima del prossimo test.

Se stai usando la tua calcolatrice grafica per aiutarti con questi grafici, assicurati di sapere quale impostazione dovresti usare e cosa significano i risultati, o la calcolatrice potrebbe darti una risposta perfettamente corretta ma “sbagliata”.

• Trova i valori anomali e i valori estremi, se presenti, per il seguente set di dati e disegna il grafico box-and-whisker. Segna eventuali valori anomali con un asterisco e qualsiasi valore estremo con un punto aperto.

Annuncio pubblicitario

Per trovare i valori anomali e valori estremi, devo prima trovare l’IQR. Dato che ci sono sette i valori dell’elenco, la mediana è il quarto valore, in modo:

Q2 = 25

La prima metà della lista è:

21, 23, 24

…quindi Q1 = 23; la seconda metà è:

29, 33, 49

…così Q3 = 33. Quindi l’IQR è dato da:

IQR = 33 – 23 = 10

I valori anomali saranno tutti i valori di seguito:

23 – 1.5×10 = 23 – 15 = 8

…o superiore:

33 + 1.5×10 = 33 + 15 = 48

I valori estremi saranno quelli sotto:

23 – 3×10 = 23 – 30 = -7

…o superiore:

33 + 3×10 = 33 + 30 = 63

Quindi ho un outlier a 49 ma nessun valore estremo. Non avrò un baffo superiore sulla mia trama perché Q3 è anche il più alto non-outlier. Quindi la mia trama assomiglia a questo:

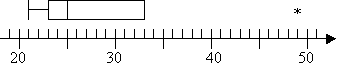
Va notato che i metodi, i termini e le regole sopra descritte sono ciò che ho insegnato e ciò che ho più comunemente visto insegnato. Tuttavia, il tuo corso potrebbe avere regole specifiche diverse o la tua calcolatrice potrebbe eseguire calcoli in modo leggermente diverso. Potrebbe essere necessario essere un po ‘ flessibile nel trovare le risposte specifiche per il tuo curriculum.