Finne Maksima og Minima ved Hjelp Av Derivater

Eksempel: en ball kastes i luften. Høyden til enhver tid t er gitt av:

h = 3 + 14t-5t2

hva er maksimal høyde?

Ved hjelp av derivater kan vi finne hellingen til den funksjonen:

h = 0 + 14 − 5 (2t)
= 14-10t

(se nedenfor dette eksemplet for hvordan vi fant det derivatet.)

finn nå når hellingen er null:

hellingen er null ved t = 1,4 sekunder

og høyden på den tiden er:

Og så:

maksimal høyde er 12,8 m (ved t = 1,4 s)

En Rask Oppfriskning På Derivater

et derivat finner i utgangspunktet hellingen til en funksjon.

i forrige eksempel tok vi dette:

h = 3 + 14t − 5t2

og kom opp med dette derivatet:

h = 0 + 14 − 5(2t)
= 14-10t

som forteller oss helningen av funksjonen til enhver tid t

vi brukte Disse Avledede Reglene:

• helningen av en konstant verdi (som 3) er 0
• helningen av en linje som 2x er 2, så 14t har en helning på 14
• en firkantet funksjon som t2 har en helning på 2t, så 5t2 har en helning på 5 (2t)
• Og så la vi dem opp: 0 + 14 − 5 (2t))

dette kalles Den Andre Derivatprøven

Andre Derivat Test

Når en funksjons helling er null ved x, og det andre derivatet ved x er:

• mindre enn 0, det er et lokalt maksimum
• større enn 0, det er et lokalt minimum
• lik 0, så mislykkes testen (det kan være andre måter å finne ut om)

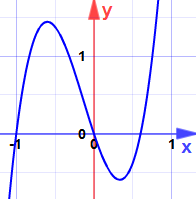
Eksempel: Finn maksima og minima for:

y = 5×3 + 2×2-3x

den deriverte (skråningen) er:

y = 15×2 + 4x− 3

som er kvadratisk med nuller på:

• x = -3/5
• x = +1/3

kan det være maksima eller minima? (Ikke se på grafen ennå!)

det andre derivatet er y» = 30x + 4

ved x = -3/5:

ved x = +1/3:

(Nå kan du se på grafen.)

et høydepunkt kalles maksimum (flertall maksima).

et lavpunkt kalles et minimum (flertall minima).

det generelle ordet for maksimum eller minimum er extremum (flertall extrema).

vi sier lokalt maksimum (eller minimum) når det kan være høyere (eller lavere) poeng andre steder, men ikke i nærheten.

Eksempel: Finn maksima og minima for:

y = x3 − 6×2 + 12x-5

derivatet er:

y = 3×2-12x + 12

Hvilken er kvadratisk med bare en null ved x = 2

er det maksimalt eller minimum?

det andre derivatet er y» = 6x − 12

ved x = 2:

og her er hvorfor:

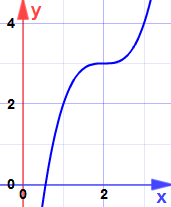
Det er et sadelpunkt … hellingen blir null, men det er verken maksimum eller minimum.

Eksempel: hva med funksjonen f(x) = |x| (absolutt verdi)?

|x / ser slik ut:

ved x=0 har den en veldig spiss forandring!

faktisk er det ikke differensierbar der (som vist på differensierbar side).

så vi kan ikke bruke denne metoden for absoluttverdifunksjonen.