als ons doel is om de relativistische veralgemening van Poissons vergelijking voor het gravitatieveld te vinden:
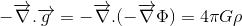
waar Φ verwijst naar de gravitatiepotentiaal en ρ naar de massadichtheid, zijn we halverwege.
inderdaad hebben we in ons vorige artikel de energie-momentum tensor gezien dat de veralgemening van de massadichtheid (rechter term van de vergelijking) overeenkomt met de energie-momentum Tµv.
het lijkt dan redelijk om aan te nemen dat onze vergelijking de vorm moet aannemen van:
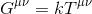
waar k staat voor een scalair en Gµv, de Einstein tensor genoemd, staat voor een rank-2 tensor die de kromming van de ruimtetijd beschrijft .
voor zover wij weten, moet de Gµv voldoen aan de volgende beperkingen::
– het moet neutraliseren, in vlakke ruimtetijd
– het moet beschrijven van de ruimte-tijd kromming en worden lineair met betrekking tot Riemann tensor
– het dient symmetrisch te zijn en rang 2 (als Tµv)
– het moet een null-divergentie (als Tµv)
– en, ten slotte, in de Newtoniaanse grenzen, moet verminderen om 4nGp
Eerste poging met de Ricci tensor als oplossing
Wij herinneren van ons artikel De Geodetische vergelijking in de Newtoniaanse Beperken dat de gravitationele potentiaal Φ is gekoppeld aan de 00-component van het gegeven via h00=(g00-1)/c2
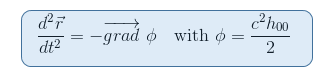
het lijkt dan natuurlijk om te zoeken naar een tensor die de tweede afgeleiden van de metriek omvat, wat het geval is voor de Riemann-tensor. Verder is de Riemann-tensor de enige kandidaat die we tot nu toe kennen om de kromming van de ruimtetijd te kunnen beschrijven (zie de tweede beperking hierboven).
omdat we een rank-2-tensor moeten vinden, en als we aannemen dat we alleen een oplossing moeten vinden in termen van de Riemann-tensor, lijkt het natuurlijk om eerst de gecontracteerde vorm van de Riemann-tensor, bekend als De Ricci-tensor, te overwegen.
om dit te zien, herinneren we aan de uitdrukking van de Riemann-tensor uit het artikel de Riemann-krommingssensor deel II: afleiding van de geodetische afwijking
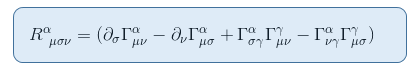
In de grens van een statisch en zwak gravitatieveld draagt slechts één term bij aan R00:
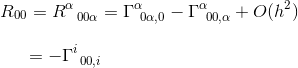
In hetzelfde artikel hebben we dit Christoffel symbool berekend en gevonden dat
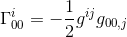
met de benadering van gij = nij en goo, j = hoo, j (zie het artikel) krijgen we:
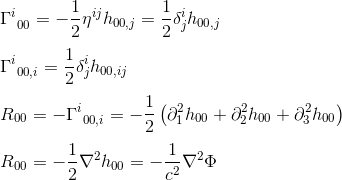
de identificatie van R00 met ΔΦ (Laplacian operator) suggereert dat de veldvergelijking in de algemene relativiteitstheorie Rab gelijk moet stellen aan een constant veelvoud van Tab.In 1915, met behulp van deze vergelijking, was Einstein zelfs in staat om het al lang bestaande probleem van Mercurius Perihelion precessie op te lossen, waardoor hij in November van dat jaar schreef: “For a few days, i was beside myself wih joyous excitement.”
uiteindelijk moest Einstein deze eerste poging afwijzen, omdat in het algemeen divergentie van Rab niet teniet wordt gedaan.
tweede poging
er is een tensor die nauw verwant is aan de Ricci scalar, die zonder tegenspraak aan de linkerkant kan worden geplaatst. Dit geeft de Einstein tensor gedefinieerd als volgt:
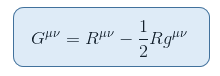
waarin R = Raa De Ricci scalaire of scalaire kromming is.
deze vorm van Gab is symmetrisch en van rank-2 en beschrijft duidelijk de kromming van de ruimtetijd. Dus het blijft gewoon om aan te tonen dat de totale afgeleide nul
is om dit te doen, beginnen we met de Bianchi identiteit
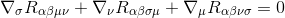
vermenigvuldigen door met gγσgαμgβν (de metrics derivaten zijn nul, dus ze fungeren als constanten en kunnen worden genomen in de derivaten), het geeft aan:
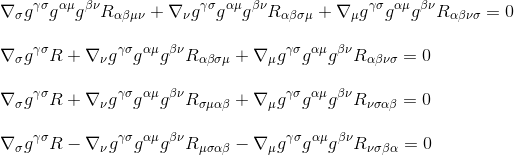
door gebruik te maken van de Ricci tensor definitie Rµv=gμβgνσRβσ (stap 3) en door de indices te hernoemen (stap 4), krijgen we
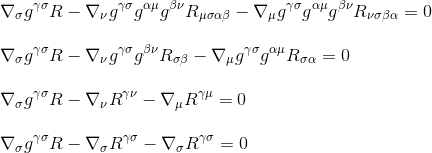
door de afgeleide te factoriseren, krijgen we uiteindelijk
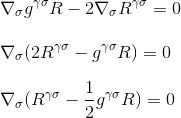
dat is precies wat we wilden aantonen: de divergentie van Einstein tensor is nul, en we hebben de juiste kandidaat gevonden voor de linkerkant van onze kromming/massa-energie vergelijking.