interkwartiel bereik & Uitschieters

• Purplemath
• MathHelp.com
• Zoek eventuele uitschieters voor de volgende gegevensverzameling:
• Zoek de uitschieters en extreme waarden, indien van toepassing, voor de volgende gegevensset, en teken de box-and-whisker plot. Markeer eventuele uitschieters met een asterisk en eventuele extreme waarden met een open punt.

Purplemath

De “inner quartile range”, afgekort “IQR”, is slechts de breedte van de box in de box-and-whisker plot. Dat wil zeggen, IQR = Q3-Q1 . De IQR kan worden gebruikt als een maat voor hoe spread-out de waarden zijn.

statistieken gaan ervan uit dat uw waarden geclusterd zijn rond een centrale waarde. De IQR vertelt hoe verspreid de “middelste” waarden zijn; het kan ook worden gebruikt om te vertellen wanneer sommige van de andere waarden zijn “te ver” van de centrale waarde. Deze” te ver weg ” punten worden “uitschieters” genoemd, omdat ze “buiten” het bereik liggen waarin we ze verwachten.

de IQR is de lengte van de box in uw box-and-whisker plot. Een uitschieter is elke waarde die meer dan anderhalf keer de lengte van de doos van beide uiteinden van de doos ligt.

inhoud gaat verder onder

MathHelp.com

dat wil zeggen, als een gegevenspunt onder Q1 – 1,5×IQR of boven Q3 + 1,5×IQR ligt, wordt het beschouwd als te ver van de centrale waarden om redelijk te zijn. Misschien stootte je de weegschaal toen je die ene meting deed, of misschien is je labpartner een idioot en had je hem nooit de apparatuur moeten laten aanraken. Wie weet? Maar wat hun oorzaak ook is, de uitschieters zijn die punten die niet lijken te “passen”.

zodra u comfortabel het vinden van de IQR bent, kunt u overgaan tot het lokaliseren van de uitschieters, indien van toepassing.

• Zoek eventuele uitschieters voor de volgende gegevensverzameling:

de waarden voor Q1-1,5×IQR en Q3 + 1,5×IQR zijn de ” hekken “die de” redelijke ” waarden markeren van de uitbijterwaarden. Uitschieters liggen buiten de hekken.

als uw opdracht niet alleen uitschieters maar ook “extreme waarden” in aanmerking neemt, dan zijn de waarden voor Q1 – 1.5×IQR en Q3 + 1,5×IQR zijn de “binnenste” hekken en de waarden voor Q1-3×IQR en Q3 + 3×IQR zijn de “buitenste” hekken.

de uitschieters (gemarkeerd met sterretjes of open stippen) bevinden zich tussen de binnen-en buitenhekken, en de uiterste waarden (gemarkeerd met het symbool dat u niet gebruikte voor de uitschieters) bevinden zich buiten de buitenhekken.

tussen haakjes, uw boek kan verwijzen naar de waarde van “1.5×IQR” als een “stap”. Dan zullen de uitschieters de getallen zijn die tussen één en twee stappen van de scharnieren liggen, en de extreme waarde zullen de getallen zijn die meer dan twee stappen van de scharnieren zijn.

kijkend naar het vorige voorbeeld, zouden de buitenhekken 14,4 – 3×0,5 = 12,9 en 14,9 + 3×0,5 = 16,4 zijn. Aangezien 16.4 recht op de bovenste buitenste omheining ligt, zou dit slechts als een uitschieter worden beschouwd, geen extreme waarde. Maar 10.2 is volledig onder de onderste buitenste omheining, dus 10.2 zou een extreme waarde zijn.

uw grafische rekenmachine kan al dan niet aangeven of een box-and-whisker plot uitschieters bevat. Het bovenstaande probleem omvat bijvoorbeeld de punten 10.2, 15.9 en 16.4 als uitschieters. Een instelling op mijn grafische rekenmachine geeft de eenvoudige box-and-whisker plot die alleen de vijf-cijferige samenvatting gebruikt, dus de verste uitschieters worden weergegeven als de eindpunten van de snorharen:

Een andere rekenmachine geeft de box-and-whisker plot met de uitschieters die speciaal gemarkeerd is (in dit geval, met een simulatie van een open punt), en de snorharen gaat alleen zo ver als de hoogste en de laagste waarden die niet uitschieters:

Mijn rekenmachine maakt geen onderscheid tussen uitschieters en extreme waarden. De jouwe misschien ook niet. Controleer uw gebruikershandleiding nu, voor de volgende test.

als u uw grafische rekenmachine gebruikt om te helpen met deze plots, zorg er dan voor dat u weet welke instelling U moet gebruiken en wat de resultaten betekenen, of de rekenmachine kan u een perfect correct maar “verkeerd” antwoord geven.

• Zoek de uitschieters en extreme waarden, indien van toepassing, voor de volgende gegevensset, en teken de box-and-whisker plot. Markeer eventuele uitschieters met een asterisk en eventuele extreme waarden met een open punt.

advertentie

om de uitschieters en extreme waarden te vinden, moet ik eerst de IQR vinden. Aangezien er zeven waarden in de lijst, de mediaan is de vierde waarde, dus:

Q2 = 25

De eerste helft van de lijst:

21, 23, 24

…dus Q1 = 23; de tweede helft is:

29, 33, 49

…dus Q3 = 33. Dan wordt de IQR gegeven door:

IQR = 33 – 23 = 10

de uitschieters zijn de waarden hieronder:

23 – 1.5×10 = 23 – 15 = 8

…of hoger:

33 + 1.5×10 = 33 + 15 = 48

de extreme waarden zijn die hieronder:

23 – 3×10 = 23 – 30 = -7

…of hoger:

33 + 3×10 = 33 + 30 = 63

dus ik heb een uitschieter op 49, maar geen extreme waarden. Ik zal geen top snorharen op mijn plot hebben omdat Q3 ook de hoogste niet-uitschieter is. Dus mijn plot ziet er zo uit:

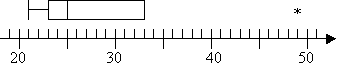
opgemerkt moet worden dat de hierboven beschreven methoden, termen en regels zijn wat ik heb onderwezen en wat ik het meest heb gezien onderwezen. Uw cursus kan echter verschillende specifieke regels hebben, of uw rekenmachine kan berekeningen iets anders doen. Het kan nodig zijn om enigszins flexibel te zijn bij het vinden van de antwoorden die specifiek zijn voor uw curriculum.