Oppervlak Traagheidsmoment-typische doorsneden i

oppervlak Traagheidsmoment of Traagheidsmoment voor een oppervlak – ook bekend als tweede oppervlak-I, is een eigenschap van vorm die wordt gebruikt om vervorming, buiging en spanning in balken te voorspellen.

Gebied traagheidsmoment – Imperial eenheden

• inches4

Gebied traagheidsmoment – Metrische eenheden

• mm4
• cm4
• m4,

Eenheden Converteren

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4.16×105 mm4 = 41.6 cm4

voorbeeld-converteren tussen Oppervlaktemoment van Traagheidseenheden

9240 cm4 kan worden omgezet in mm4 door te vermenigvuldigen met 104

(9240 cm4) 104 = 9.24 107 mm4

Gebied traagheidsmoment (traagheidsmoment voor een Gebied of een Tweede Moment van de Omgeving)

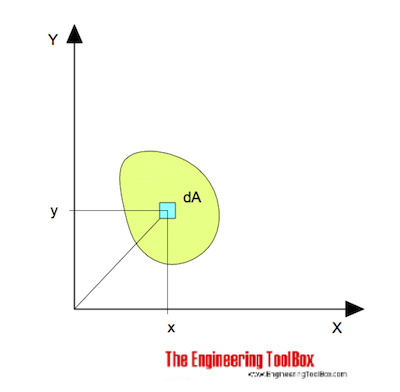
voor het buigen van rond de x-as kan worden uitgedrukt als

Ix = ∫ y 2 dA (1)

waar

Ix = Gebied traagheidsmoment in verband met de x-as (m4, mm4, inches4)

y = de loodrechte afstand van de x-as van het element dA (m, mm, inch)

dA = een elemental oppervlakte (m2, mm2, inches2)

Het traagheidsmoment voor het buigen van rond de y-as kan worden uitgedrukt als

Iy = ∫ x2 dA (2)

waar

Iy = Gebied traagheidsmoment in verband met de y-as (m4, mm4, inches4)

x = de loodrechte afstand van de as aan de y-element dA (m, mm, inch)

Gebied traagheidsmoment voor typische doorsnede I

• Gebied traagheidsmoment voor typische doorsnede II

Solide Vierkante doorsnede

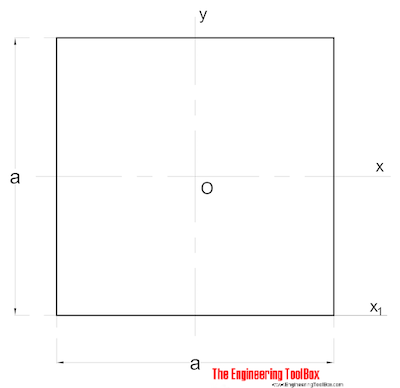
Het Gebied traagheidsmoment voor een solide vierkante doorsnede kan worden berekend als

Ix = a4 / 12 (2)

waarbij

a = zijde (mm, m, in..)

Iy = a4 / 12 (2b)

Stevige Rechthoekige doorsnede

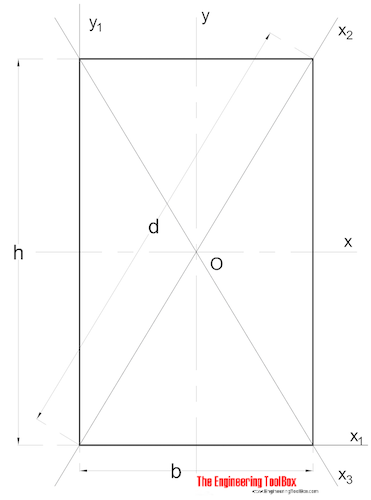
De Omgeving Moment van Ineria voor een rechthoekige doorsnede, kan worden berekend als

Ix = b h3 / 12 (3)

waar

b = breedte

h = hoogte

Iy = b3 h / 12 (3b)

Gevulde Cirkelvormige doorsnede

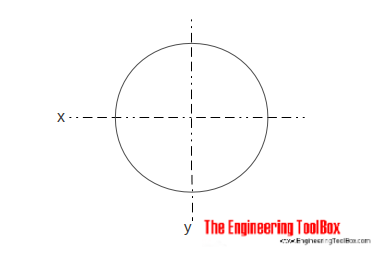
Het Gebied traagheidsmoment voor een solide cilindrisch gedeelte kan worden berekend als

Ix = π r4 / 4

= π d4 / 64 (4)

waar

r = straal

d = diameter

Iy = π r4 / 4

= π d4 / 64 (4b)

Holle Cilindrische doorsnede

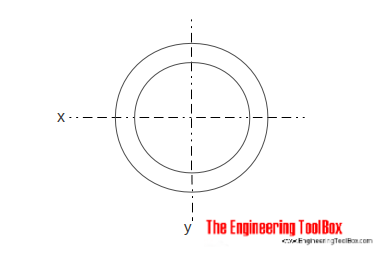
Het Gebied traagheidsmoment voor een holle cilindrische gedeelte kan worden berekend als

Ix = π (do4 – di4) / 64 (5)

waar

doen = cilinder buiten diameter

di = binnen diameter cilinder

Iy = π (do4 – di4) / 64 (5b)

Vierkante doorsnede – Diagonale momenten

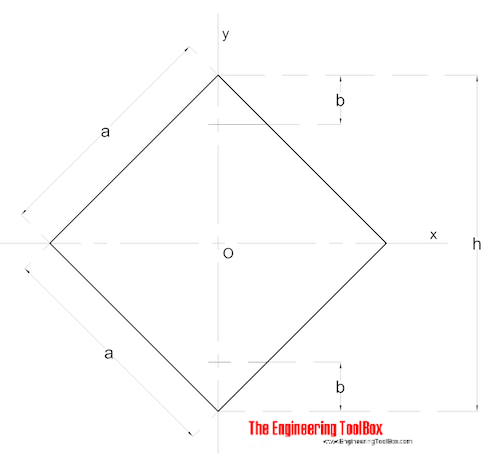
het diagonaal traagheidsmomenten voor een vierkant gedeelte kunnen worden berekend als

Ix = Iy = a4 / 12 (6)

rechthoekige doorsnede-gebied momenten op elke lijn door zwaartepunt

rechthoekige doorsnede en gebied van Moment op lijn door zwaartepunt kan worden berekend als

Ix = (b h / 12) (H2 cos2 A + b2 sin2 a) (7)

symmetrische vorm

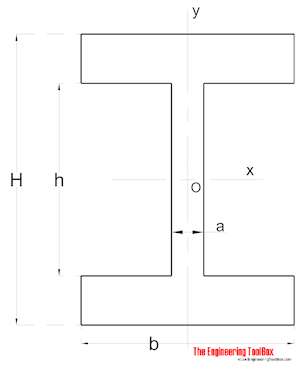
Traagheidsmoment voor a symmetrische vorm kan worden berekend als

Ix = (a h3 / 12) + (b / 12) (H3 – h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

Nonsymmetrical Vorm

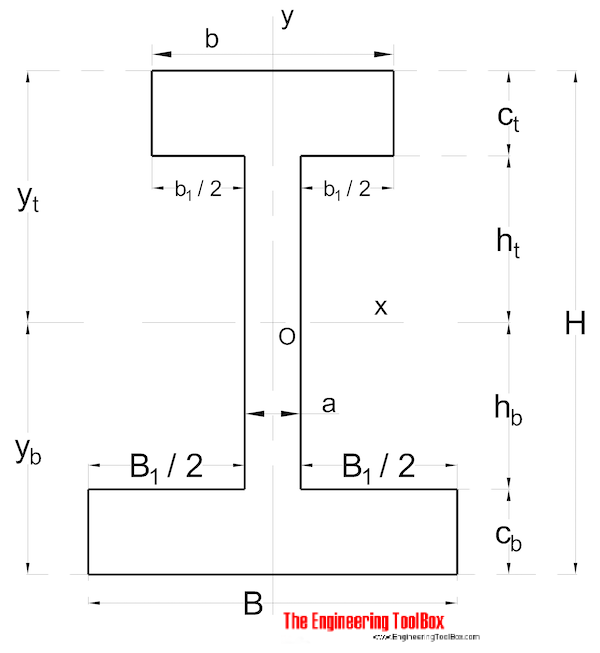
Gebied traagheidsmoment voor een niet symmetrische vorm kan worden berekend als

Ix = (1 / 3) (B yb3 – B1 hb3 + b yt3 – b1 ht3) (9)

• Gebied traagheidsmoment voor typische doorsnede II

Gebied traagheidsmoment t.o.v. Polair traagheidsmoment t.o.v. Moment van inertie

• “oppervlakte traagheidsmoment” is een eigenschap van vorm die wordt gebruikt om vervorming, buiging en spanning in bundels
• “polair Traagheidsmoment” te voorspellen als een maat voor het vermogen van een bundel om torsie te weerstaan – die nodig is om de draai te berekenen van een bundel die aan koppel
• wordt onderworpen”traagheidsmoment” is een maat voor de weerstand van een object tegen verandering in draairichting.

Sectiemodulus

• de “Sectiemodulus” wordt gedefinieerd als W = I / y, waarbij I het traagheidsmoment is en y de afstand is van de neutrale as tot een bepaalde vezel