onde está uma função em um ponto alto ou baixo? O cálculo pode ajudar!
um máximo é um ponto alto e um mínimo é um ponto baixo:

numa função em mudança suave, um máximo ou mínimo é sempre quando a função se achata (exceto para um ponto de sela).
onde é que ele esmaece? Onde a inclinação é zero.
onde está o declive zero? O derivado diz-nos!
vamos mergulhar com um exemplo:

- exemplo: uma bola é lançada no ar. A sua altura a qualquer momento t é dada por:
- Qual é a sua altura máxima?Usando derivados podemos encontrar o declive dessa função:
- Uma Rápida atualização sobre Derivativos
- como sabemos que é um máximo (ou mínimo)?
- segundo teste derivado
- Exemplo: Encontrar valores máximos e mínimos para:
- Palavras
- mais um exemplo
- exemplo: encontrar os máximos e mínimos para:
- deve ser diferenciável
- exemplo: que tal a função f(x) = |x| (valor absoluto) ?
exemplo: uma bola é lançada no ar. A sua altura a qualquer momento t é dada por:
h = 3 + 14t-5t2
Qual é a sua altura máxima?Usando derivados podemos encontrar o declive dessa função:
![]() h = 0 + 14 − 5 (2t)
h = 0 + 14 − 5 (2t)
= 14-10t
(veja abaixo este exemplo para como encontramos esse derivado.)

encontra − se agora quando o declive é zero:
A inclinação é zero em t = 1,4 segundos
E a altura em que o tempo é:
E assim:
A altura máxima é de 12,8 m (t = 1.4 s)
Uma Rápida atualização sobre Derivativos
Um derivado basicamente encontrar a inclinação de uma função.
no exemplo anterior nós tomamos este:
h = 3 + 14t-5t2
e surgiu com este derivado:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
o Que nos diz o declive da função em qualquer tempo t
usamos esses Derivados Regras:
- A inclinação de um valor constante (3) seja 0
- A inclinação de uma linha como 2x é 2, então 14t tem uma inclinação de 14
- Um quadrado função como t2 tem uma inclinação de 2t, então, 5t2 tem uma inclinação de 5(2t)
- E, em seguida, adicionamos-los: 0 + 14 − 5 (2t)
como sabemos que é um máximo (ou mínimo)?
vimos no gráfico! Mas fora isso … derivatives vêm em Socorro novamente.
Tomar a derivada da curva (a segunda derivada da função original):
A Derivada de 14 − 10t é -10
Isso significa que o declive é continuamente ficando menor (-10): viajar, da esquerda para a direita, a inclinação começa positivo (a função sobe), passa por zero (o plano ponto) e, em seguida, a inclinação torna-se negativo (função cair):

um declive que fica menor (e vai embora 0) significa um máximo.
este é chamado o segundo teste derivado
no gráfico acima i mostrou o declive antes e depois, mas na prática fazemos o teste no ponto onde o declive é zero:
segundo teste derivado
quando o declive de uma função é zero em x, e o segundo derivado em x é:
- menor que 0, ele é um máximo local
- maior que 0, é um mínimo local
- igual a 0, então o teste falha (pode haver outras maneiras de descobrir que)
“Segunda Derivada: menor que 0, no máximo, maior que 0 é o mínimo”
Exemplo: Encontrar valores máximos e mínimos para:
y = 5×3 + 2×2 − 3x
A derivada (inclinação) é:
![]() y = 15×2 + 4x− 3
y = 15×2 + 4x− 3
o Que é quadrática com zeros:
- x = -3/5
- x = +1/3
podem ser maxima ou minima? (Não olhe para o gráfico ainda!)
A segunda derivada é y” = 30x + 4
Em x = -3/5:
Em x = +1/3:
(Agora você pode olhar para o gráfico.)
Palavras
Um ponto alto é chamado de máximo (plural maxima).
um ponto baixo é chamado de mínimo (plural minima).
a palavra geral para máximo ou mínimo é extremum (plural extremos).
dizemos máximo local (ou mínimo) quando pode haver pontos mais altos (ou mais baixos) em outros lugares, mas não nas proximidades.
mais um exemplo
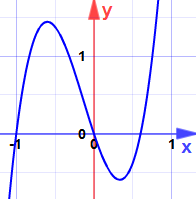
exemplo: encontrar os máximos e mínimos para:
y = x3-6×2 + 12x − 5
o derivado é:
![]() y = 3×2-12x + 12
y = 3×2-12x + 12
que é quadrático com apenas um zero a x = 2
é um máximo ou mínimo?
A segunda derivada é y” = 6x − 12
Em x = 2:
E aqui está o porquê:
É um ponto de sela … o declive torna-se zero, mas não é um máximo ou mínimo.
deve ser diferenciável
e há um importante ponto técnico:
a função deve ser diferenciável (a derivada deve existir em cada ponto do seu domínio).
exemplo: que tal a função f(x) = |x| (valor absoluto) ?
| |x| olha como esta: |  |
Em x=0 tem uma muito pontudo mudar!
na verdade não é diferenciável lá (como mostrado na página diferenciável).
então não podemos usar este método para a função valor absoluto.
a função também deve ser contínua, mas qualquer função que seja diferenciável também é contínua, por isso não precisa se preocupar com isso.
