
















Timsort: en mycket snabb , o(n log n), stabil sorteringsalgoritm byggd för den verkliga världen — inte konstruerad i akademin.
Klicka här för att se den uppdaterade artikeln:

Timsort är en sorteringsalgoritm som är effektiv för verkliga data och inte skapad i ett akademiskt laboratorium. Tim Peters skapade Timsort för programmeringsspråket Python 2001. Timsort analyserar först listan som den försöker sortera och väljer sedan ett tillvägagångssätt baserat på analysen av listan.
sedan algoritmen har uppfunnits har den använts som standardsorteringsalgoritm i Python, Java, Android-plattformen och i GNU Octave.
Timsorts stora O-notation är O (n log n). För att lära dig om Big O notation, Läs detta.

Timsorts sorteringstid är densamma som Mergesort, vilket är snabbare än de flesta andra sorter du kanske vet. Timsort använder sig faktiskt av Insättningsort och Mergesort, som du kommer att se snart.
Peters utformade Timsort för att använda redan beställda element som finns i de flesta verkliga datamängder. Det kallar dessa redan beställda element”naturliga körningar”. Det itererar över data som samlar in elementen i körningar och samtidigt sammanfogar dessa körningar i en.
matrisen har färre än 64 element i den
om matrisen vi försöker sortera har färre än 64 element i den, kommer Timsort att utföra en insättningsort.
en insättningsort är en enkel sort som är mest effektiv på små listor. Det är ganska långsamt på större listor, men mycket snabbt med små listor. Tanken med en insättningsort är som följer:
- titta på element en efter en
- Bygg upp sorterad lista genom att infoga elementet på rätt plats
här är en spårtabell som visar hur insertion sort skulle sortera listan

i det här fallet sätter vi in de nyligen sorterade elementen i en ny undermatris, som börjar i början av arrayen.
här är en gif som visar insättningsort:
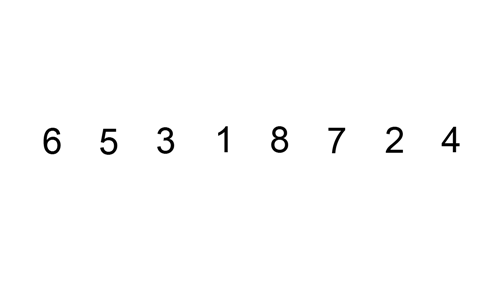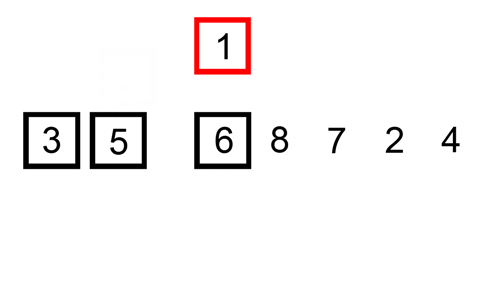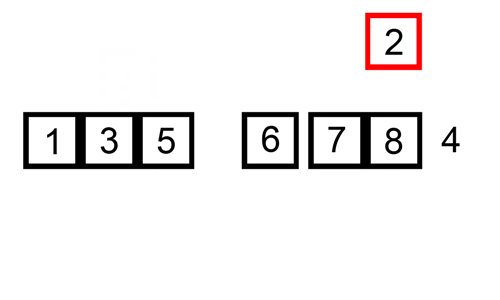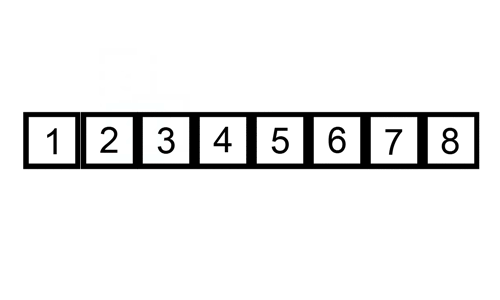
mer om körningar
om listan är större än 64 element än algoritmen kommer att göra ett första pass genom listan letar efter delar som strikt ökar eller minskar. Om delen minskar kommer den att vända den delen.
så om körningen minskar ser den ut så här (där körningen är i fetstil):

om det inte minskar ser det ut så här:

minrun är en storlek som bestäms baserat på arrayens storlek. Algoritmen väljer den så att de flesta körningar i en slumpmässig array är, eller blir minrun, i längd. Sammanslagning av 2 arrayer är effektivare när antalet körningar är lika med eller något mindre än en effekt på två. Timsort väljer minrun för att försöka säkerställa denna effektivitet genom att se till att minrun är lika med eller mindre än en effekt på två.
algoritmen väljer minrun från intervallet 32 till 64 inklusive. Den väljer minrun så att längden på den ursprungliga matrisen, när den divideras med minrun, är lika med eller något mindre än en effekt på två.
om längden på körningen är mindre än minrun beräknar du längden på den körningen från minrun. Med det här nya numret tar du så många objekt före körningen och utför en insättningsort för att skapa en ny körning.
så om minrun är 63 och längden på körningen är 33, gör du 63-33 = 30. Du tar sedan 30 element framför slutet av körningen, så det här är 30 objekt från kör och utför sedan en infogningssort för att skapa en ny körning.
efter att denna del har slutförts borde vi nu ha en massa sorterade körningar i en lista.
sammanslagning

Timsort utför nu mergesort för att slå samman körningarna tillsammans. Timsort ser dock till att upprätthålla stabilitet och sammanfoga balans medan sammanfoga sortering.
för att upprätthålla stabilitet bör vi inte byta 2 nummer av lika värde. Detta håller inte bara sina ursprungliga positioner i listan utan gör det möjligt för algoritmen att bli snabbare. Vi kommer inom kort att diskutera sammanslagningsbalansen.
när Timsort hittar körningar lägger den till dem i en stapel. En enkel stack skulle se ut så här:

Föreställ dig en stapel plattor. Du kan inte ta tallrikar från botten, så du måste ta dem från toppen. Detsamma gäller för en stapel.
Timsort försöker balansera två konkurrerande behov när mergesort körs. Å ena sidan vill vi fördröja sammanslagningen så länge som möjligt för att utnyttja mönster som kan komma upp senare. Men vi skulle vilja ha ännu mer att göra sammanslagningen så snart som möjligt för att utnyttja den körning som körningen just hittat är fortfarande hög i minneshierarkin. Vi kan inte heller fördröja sammanslagning” för länge ” eftersom det förbrukar minne för att komma ihåg de körningar som fortfarande är unmerged, och stacken har en fast storlek.
för att säkerställa att vi har denna kompromiss håller Timsort reda på de tre senaste artiklarna på stacken och skapar två lagar som måste gälla för dessa artiklar:
1. A > B + C
2. B > C
där A, B och C är de tre senaste objekten på stacken.
för att citera Tim Peters själv:
vad som visade sig vara en bra kompromiss upprätthåller två invarianter på stapelposterna, där A, B och C är längderna på de tre högsta ännu inte sammanslagna skivorna
vanligtvis är det svårt att slå samman intilliggande körningar av olika längder på plats. Det som gör det ännu svårare är att vi måste upprätthålla stabiliteten. För att komma runt detta avsätter Timsort tillfälligt minne. Det placerar de mindre (kallar båda körningarna A och B) av de två körningarna i det tillfälliga minnet.
galopperande

medan Timsort slår samman A och B märker det att en körning har ”vunnit” många gånger i rad. Om det visade sig att Kör a bestod av helt mindre antal än kör B skulle kör A hamna tillbaka på sin ursprungliga plats. Att slå samman de två körningarna skulle innebära mycket arbete för att inte uppnå någonting.
oftare än inte, data kommer att ha någon redan existerande intern struktur. Timsort antar att om många kör A: S värden är lägre än kör B: s värden, är det troligt att A fortsätter att ha mindre värden än B.
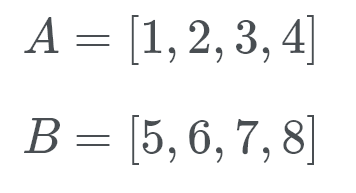
Timsort går sedan in i galoppläge. Istället för att kontrollera A och B mot varandra utför Timsort en binär sökning efter lämplig position för b i a. på så sätt kan Timsort flytta en hel del av A på plats. Sedan söker Timsort efter lämplig plats för A I B. Timsort flyttar sedan en hel del av B can på en gång och på plats.
Låt oss se detta i aktion. Timsort kontrollerar B (vilket är 5) och med hjälp av en binär sökning Letar den efter rätt plats i A.
Tja, B hör till baksidan av listan över A. nu kontrollerar Timsort efter A (vilket är 1) på rätt plats för B. Så vi letar efter var nummer 1 går. Detta nummer går i början av B. Vi vet nu att B tillhör i slutet av A och A tillhör i början av B.
det visar sig att denna operation inte är värt det om lämplig plats för B ligger mycket nära början av A (eller vice versa). så gallop-läget går snabbt ut om det inte lönar sig. Dessutom noterar Timsort och gör det svårare att gå in i galoppläge senare genom att öka antalet på varandra följande A-bara eller B-bara vinster som krävs för att komma in. Om gallop-läget lönar sig, gör Timsort det lättare att återinträda.
kort sagt, Timsort gör 2 saker otroligt bra:
- bra prestanda på arrayer med befintlig intern struktur
- att kunna upprätthålla en stabil sortering
tidigare, för att uppnå en stabil sortering, måste du zip objekten i din lista upp med heltal och sortera det som en rad tupler.
kod
om du inte är intresserad av koden kan du hoppa över den här delen. Det finns lite mer information under detta avsnitt.
källkoden nedan är baserad på min och Nanda Javarmas arbete. Källkoden är inte komplett och liknar inte heller Pythons officiella sorterade() källkod. Detta är bara en dumbed-down Timsort jag genomfört för att få en allmän känsla av Timsort. Om du vill se Timsorts ursprungliga källkod i all sin härlighet, kolla in den här. Timsort implementeras officiellt i C, inte Python.
Timsort är faktiskt inbyggt i Python, så den här koden fungerar bara som en förklarare. För att använda Timsort helt enkelt skriva:
list.sort()
eller
sorted(list)
om du vill behärska hur Timsort fungerar och få en känsla för det, föreslår jag starkt att du försöker implementera det själv!
denna artikel är baserad på Tim Peters ursprungliga introduktion till Timsort, finns här.