Wo befindet sich eine Funktion an einem hohen oder niedrigen Punkt? Kalkül kann helfen!
Ein Maximum ist ein Höhepunkt und ein Minimum ist ein Tiefpunkt:

In einer sich reibungslos ändernden Funktion ist ein Maximum oder Minimum immer dort, wo die Funktion abgeflacht ist (mit Ausnahme eines Sattelpunkts).
Wo wird es flach? Wo die Steigung Null ist.
Wo ist die Steigung Null? Das Derivat sagt es uns!
Lassen Sie uns gleich mit einem Beispiel eintauchen:
- Beispiel: Ein Ball wird in die Luft geworfen. Seine Höhe zu jeder Zeit t ist gegeben durch:
- Was ist seine maximale Höhe?
- Eine kurze Auffrischung der Ableitungen
- Woher wissen wir, dass es ein Maximum (oder Minimum) ist?
- Zweiter Ableitungstest
- Beispiel: Finden Sie die Maxima und Minima für:
- Wörter
- Ein weiteres Beispiel
- Beispiel: Finden Sie die Maxima und Minima für:
- Muss differenzierbar sein
- Beispiel: Wie wäre es mit der Funktion f(x) = |x| (absoluter Wert)?
Beispiel: Ein Ball wird in die Luft geworfen. Seine Höhe zu jeder Zeit t ist gegeben durch:
h = 3 + 14t – 5t2
Was ist seine maximale Höhe?
Mit Derivaten können wir die Steigung dieser Funktion finden:
![]() h = 0 + 14 − 5 (2t)
h = 0 + 14 − 5 (2t)
= 14 – 10t
(Siehe unten in diesem Beispiel, wie wir diese Ableitung gefunden haben.)
Finden Sie nun, wenn die Steigung Null ist:
Die Steigung ist Null bei t = 1,4 Sekunden
Und die Höhe zu diesem Zeitpunkt ist:
Und so:
Die maximale Höhe beträgt 12,8 m (bei t = 1,4 s)
Eine kurze Auffrischung der Ableitungen
Eine Ableitung findet grundsätzlich die Steigung einer Funktion.
Im vorherigen Beispiel haben wir Folgendes genommen:
h = 3 + 14t – 5t2
und diese Ableitung entwickelt:
![]() h = 0 + 14 − 5 (2t)
h = 0 + 14 − 5 (2t)
= 14 – 10t
Das sagt uns die Steigung der Funktion zu jeder Zeit t
Wir haben diese abgeleiteten Regeln verwendet:
- Die Steigung eines konstanten Wertes (wie 3) ist 0
- Die Steigung einer Linie wie 2x ist 2, also hat 14t eine Steigung von 14
- Eine quadratische Funktion wie t2 hat eine Steigung von 2t, also hat 5t2 eine Steigung von 5(2t)
- Und dann haben wir sie addiert: 0 + 14 − 5 (2t)
Woher wissen wir, dass es ein Maximum (oder Minimum) ist?
Wir haben es in der Grafik gesehen! Aber sonst … derivate kommen wieder zur Rettung.
Nehmen Sie die Ableitung der Steigung (die zweite Ableitung der ursprünglichen Funktion):
Die Ableitung von 14 – 10t ist -10
Dies bedeutet, dass die Steigung kontinuierlich kleiner wird (-10): Von links nach rechts beginnt die Steigung positiv (die Funktion steigt), geht durch Null (der flache Punkt) und dann wird die Steigung negativ (die Funktion fällt):

Eine Steigung, die kleiner wird (und durch 0 geht), bedeutet ein Maximum.
Dies wird als zweiter Ableitungstest bezeichnet
In der obigen Grafik habe ich die Steigung vorher und nachher gezeigt, aber in der Praxis führen wir den Test an dem Punkt durch, an dem die Steigung Null ist:
Zweiter Ableitungstest
Wenn die Steigung einer Funktion bei x Null ist und die zweite Ableitung bei x:
- kleiner als 0, es ist ein lokales Maximum
- größer als 0, es ist ein lokales Minimum
- gleich 0, dann schlägt der Test fehl (es kann jedoch andere Möglichkeiten geben, dies herauszufinden)
“ Zweite Ableitung: Kleiner als 0 ist ein Maximum, größer als 0 ist ein Minimum“
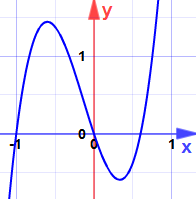
Beispiel: Finden Sie die Maxima und Minima für:
y = 5×3 + 2×2 – 3x
Die Ableitung (Steigung) ist:
![]() y = 15×2 + 4x − 3
y = 15×2 + 4x − 3
Welches ist quadratisch mit Nullen bei:
- x = -3/5
- x = +1/3
Können es Maxima oder Minima sein? (Schau dir die Grafik noch nicht an!)
Die zweite Ableitung ist y“ = 30x + 4
Bei x = -3/5:
Bei x = +1/3:
(Jetzt können Sie sich die Grafik ansehen.)
Wörter
Ein Höhepunkt wird als Maximum bezeichnet (Plural Maxima).
Ein Tiefpunkt wird als Minimum (Plural Minima) bezeichnet.
Das allgemeine Wort für Maximum oder Minimum ist extremum (Plural extrema).
Wir sagen lokales Maximum (oder Minimum), wenn es anderswo höhere (oder niedrigere) Punkte gibt, aber nicht in der Nähe.
Ein weiteres Beispiel
Beispiel: Finden Sie die Maxima und Minima für:
y = x3 – 6×2 + 12x – 5
Die Ableitung lautet:
![]() y = 3×2 – 12x + 12
y = 3×2 – 12x + 12
Welches ist quadratisch mit nur einer Null bei x = 2
Ist es ein Maximum oder Minimum?
Die zweite Ableitung ist y“ = 6x – 12
Bei x = 2:
Und hier ist der Grund:
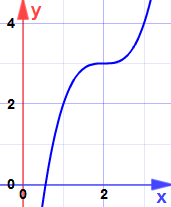
Es ist ein Sattelpunkt … die Steigung wird zwar Null, ist aber weder maximal noch minimal.
Muss differenzierbar sein
Und es gibt einen wichtigen technischen Punkt:
Die Funktion muss differenzierbar sein (die Ableitung muss an jedem Punkt in ihrer Domäne existieren).
Beispiel: Wie wäre es mit der Funktion f(x) = |x| (absoluter Wert)?
| | x / sieht so aus: |  |
Bei x = 0 hat es eine sehr spitze Veränderung!
Tatsächlich ist es dort nicht differenzierbar (wie auf der differenzierbaren Seite gezeigt).
Daher können wir diese Methode nicht für die Absolutwertfunktion verwenden.
Die Funktion muss ebenfalls kontinuierlich sein, aber jede Funktion, die differenzierbar ist, ist auch kontinuierlich, sodass Sie sich darüber keine Sorgen machen müssen.


