tai: miten välttää polynomin pitkä jako löydettäessä tekijöitä
Muistatko tehneesi jakolaskun Aritmetiikassa?
”7 jaettuna 2: lla on yhtä kuin 3, jonka loppuosa on 1”
jokaisella jaon osalla on nimet:
, joka voidaan kirjoittaa uudelleen summana näin:
Polynomit
No, voimme myös jakaa polynomit.
f (x) œ (x) = q (x), jonka loppuosa on R (x)
, mutta on parempi kirjoittaa se summana näin:
kuten tässä esimerkissä käyttäen polynomi pitkä jako:
esimerkki: 2×2−5x-1 jaettuna x: llä−3
- f (x) on 2×2-5x-1
- d (x) on x−3
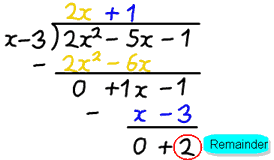
jakamisen jälkeen saamme vastauksen 2x+1, mutta jäljellä on 2.
- q (x) on 2x+1
- r (x) is 2
tyyliin f (x) = d (x)·q (x) + r (x) voidaan kirjoittaa:
2×2−5x−1 = (x−3)(2x+1) + 2
mutta sinun täytyy tietää Vielä yksi asia.:
aste r (x) on aina pienempi kuin d (x)
sanotaan, että jaamme asteen 1 polynomilla (kuten ”x−3”) loppuosalla on aste 0 (toisin sanoen vakio, kuten ”4”).
käytämme tätä ajatusta ”jäljellä olevassa lauseessa”:
jäljellä oleva lause
kun jaamme f (x) yksinkertaisella polynomilla x-c saamme:
f(x) = (x-c· * q (x) + r (x)
x-c on aste 1, joten r(x): llä täytyy olla aste 0, joten se on vain jokin vakio r:
f (x) = (x−c)·q (x) + r
nyt nähdään mitä tapahtuu, kun meillä on X yhtä suuri kuin c:
näin saadaan:
loppulause:
kun jaamme polynomin f (x) X−c: llä, loppuosa on f (c)
joten löytää loput jälkeen jakamalla X-c meidän ei tarvitse tehdä mitään jakoa:
laske vain f (c).
katsotaan, että käytännössä:
esimerkki: loput 2×2−5x−1: n jälkeen jaetaan x−3: lla
(esimerkkimme ylhäältä)
meidän ei tarvitse jakaa (x−3: lla) … laske vain f(3):
2(3)2-5(3)-1 = 2×9-5×3−1
= 18-15-1
= 2
ja se on loput saimme meidän laskelmat edellä.
meidän ei tarvinnut tehdä pitkää jakoa ollenkaan!
esimerkki: Loput 2×2−5x−1: n jälkeen jaetaan x−5: llä
sama esimerkki kuin edellä, mutta tällä kertaa jaamme ”x−5”
”c” on 5, joten tarkistakaamme f(5):
2(5)2-5(5)-1 = 2×25-5×5−1
= 50-25-1
= 24
loppuosa on 24
jälleen kerran … Ei tarvinnut tehdä pitkää jakoa löytääksemme sen.
Tekijälause
Nyt …
mitä jos lasketaan f (c) ja se on 0?
… se tarkoittaa, että loput on 0, ja …
… (x-c) on oltava tekijä, polynomi!
näemme tämän, kun jaetaan kokonaislukuja. Esimerkiksi 60 œ20 = 3 ilman jäljellä. 20 on siis kerroin 60.
esimerkki: x2−3x-4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
joten (x−4) on oltava tekijä x2-3x−4
ja niin olemme:
Tekijälause:
kun f (c)=0 niin X-c on tekijä f (x)
ja toisinpäin myös:
kun x-c on tekijä f (x) sitten F (c)=0
miksi tämä on hyödyllistä?
tieto siitä, että x−c on tekijä, on sama kuin tieto siitä, että c on juuri (ja päinvastoin).
tekijä ”x−c” ja juuri ”C” ovat sama asia
tietää yhden ja me tiedämme toisen
yhden asian osalta se tarkoittaa, että voimme nopeasti tarkistaa, onko (x-c) jokin polynomin tekijä.
esimerkki: Etsi tekijät 2×3−x2−7x+2
polynomi on aste 3, ja sitä voi olla vaikea ratkaista. Juonikaamme se ensin.:
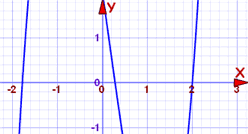
käyrä ylittää x-akselin kolmessa pisteessä, ja yksi niistä voi olla 2. Voimme tarkistaa helposti:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Kyllä! f (2)=0, joten olemme löytäneet juuri ja tekijä.
joten (x−2) on oltava kerroin 2×3-x2-7x+2
entä missä se ylittää lähellä -1,8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Ei, (x+1,8) ei ole tekijä. Voisimme kokeilla muita arvoja lähellä ja ehkä onnistaa.
mutta ainakin tiedämme (x−2) olevan tekijä, joten käytetään polynomin pitkää jakoa:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
loppu on odotetusti nolla.
vielä parempi on, että jäljelle jää neliöyhtälö 2×2+3x−1, joka on helppo ratkaista.
sen juuret ovat -1,78… ja 0,28…, joten lopputulos on:
2×3−x2−7x+2 = (x-2)(x+1,78…) (x−0, 28…)
pystyimme ratkaisemaan vaikean polynomin.
Yhteenveto
loppulause:
- kun jaamme polynomin f (x) X−c: llä, loppuosa on f (c)
Tekijälause:
- kun f (c)=0 niin X-c on tekijä f (x)
- kun x-c on tekijä f (x) niin F (c)=0



