Oppure: come evitare la divisione lunga polinomiale quando si trovano i fattori
Ti ricordi di fare la divisione in aritmetica?
“7 diviso 2 è uguale a 3 con resto di 1”
Ogni parte della divisione ha nomi:
Che può essere riscritto come somma come questo:
Polinomi
Beh, si può dividere in due polinomi.
f(x) ś d(x) = q(x) con un resto r(x)
Ma è meglio scriverlo come somma di simile a questo:
Come in questo esempio, utilizzando il Polinomio di Divisione Lunga:
Esempio: 2×2−5x−1 diviso per x−3
- f(x) è 2×2−5x−1
- d(x) è x−3
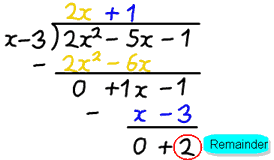
Dopo la divisione otteniamo la risposta 2x+1, ma c’è un resto di 2.
- q(x) 2x+1
- r(x) è 2
In stile f(x) = d(x)·q(x) + r(x), si può scrivere:
2×2−5x−1 = (x−3)(2x+1) + 2
Ma avete bisogno di sapere una cosa in più:
Il grado di r(x) è sempre minore di d(x)
Dire che ci divide da un polinomio di grado 1 (ad esempio “x 3”) il resto sarà il grado 0 (in altre parole una costante, come “4”).
Useremo questa idea nel “Teorema del resto”:
Il Teorema del resto
Quando dividiamo f (x) per il semplice polinomio x-c otteniamo:
f(x) = (x−c)·q(x) + r(x)
x−c è di grado 1, quindi r(x) deve avere il grado 0, quindi è solo una costante r :
f(x) = (x−c)·q(x) + r
Ora vedi cosa succede quando si ha x uguale a c:
Quindi, questo è:
Il Resto Teorema:
Quando dobbiamo dividere un polinomio f(x) da x−c il resto è f(c)
Quindi, per trovare il resto della divisione di x-c non abbiamo bisogno di fare la divisione:
Basta calcolare f (c).
Vediamo che in pratica:
Esempio: Il resto dopo 2×2-5x−1 è diviso per x−3
(il nostro esempio dall’alto)
Non abbiamo bisogno di dividere per (x-3) … basta calcolare f(3):
2(3)2-5(3)-1 = 2×9−5×3−1
= 18-15-1
= 2
E questo è il resto che abbiamo ottenuto dai nostri calcoli di cui sopra.
Non avevamo bisogno di fare una lunga divisione!
Esempio: Il resto dopo 2×2−5x−1 è diviso da x−5
Stesso esempio di sopra, ma questa volta ci dividono “x−5”
“c” è 5, quindi cerchiamo di controllare le f(5):
2(5)2-5(5)-1 = 2×25−5×5−1
= 50-25-1
= 24
Il resto è di 24
ancora una Volta … Non abbiamo avuto bisogno di fare Lunghe divisioni per scoprirlo.
Il teorema del fattore
Ora …
Cosa succede se calcoliamo f (c) ed è 0?
… ciò significa che il resto è 0 e …
… (x-c) deve essere un fattore del polinomio!
Lo vediamo quando dividiamo numeri interi. Ad esempio 60 ÷ 20 = 3 senza resto. Quindi 20 deve essere un fattore di 60.
Esempio: x2−3x−4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
quindi (x−4), deve essere un fattore x2−3x−4
E così abbiamo:
Il Fattore Teorema:
se f(c)=0 allora x−c è un fattore di f(x)
E l’altro senso intorno, troppo:
Quando x−c è un fattore di f(x) allora f(c)=0
Perché È Utile?
Sapere che x−c è un fattore equivale a sapere che c è una radice (e viceversa).
Il fattore “x−c” e la radice “c” sono la stessa cosa
Conosci uno e conosciamo l’altro
Per prima cosa, significa che possiamo verificare rapidamente se (x−c) è un fattore del polinomio.
Esempio: Trova i fattori di 2×3−x2−7x+2
Il polinomio è di grado 3 e potrebbe essere difficile da risolvere. Quindi cerchiamo di tracciare prima:
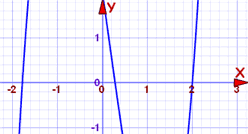
La curva attraversa l’asse x in tre punti, e uno di essi potrebbe essere a 2. Possiamo controllare facilmente:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Sì! f (2)=0, quindi abbiamo trovato una radice e un fattore.
Quindi (x−2) deve essere un fattore di 2×3-x2-7x+2
Che ne dici di dove attraversa vicino a -1.8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
No, (x+1.8) non è un fattore. Potremmo provare altri valori nelle vicinanze e magari avere fortuna.
Ma almeno sappiamo (x−2) è un fattore, quindi usiamo la divisione lunga polinomiale:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
Come previsto il resto è zero.
Meglio ancora, ci rimane l’equazione quadratica 2×2+3x – 1 che è facile da risolvere.
Le sue radici sono -1.78… e 0,28…, quindi il risultato finale è:
2×3−x2−7x+2 = (x−2) (x+1.78…) (x−0.28…)
Siamo stati in grado di risolvere un polinomio difficile.
Sommario
Il Resto il Teorema di:
- Quando dobbiamo dividere un polinomio f(x) per x−c il resto è f(c)
Il Fattore di Teorema:
- se f(c)=0, allora x−c è un fattore di f(x)
- Quando x−c è un fattore di f(x) allora f(c)=0



