O: cómo evitar la División Larga Polinómica al encontrar factores
¿Recuerda haber hecho división en Aritmética?
«7 dividido por 2 es igual a 3 con un resto de 1»
Cada parte de la división tiene nombres:

Que se puede reescribir como una suma como esta:
Polinomios
Bueno, también podemos dividir polinomios.
f(x) ÷ d(x) = q(x) con un resto r(x)
Pero es mejor escribir como una suma como este:
Como en este ejemplo, utilizando el Polinomio de la División Larga:
Ejemplo: 2×2−5x−1 dividido por x−3
- f(x) 2×2−5x−1
- d(x) es x−3
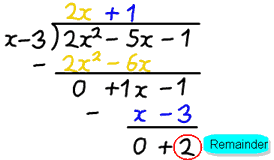
Después de dividir obtenemos la respuesta 2x+1, pero hay un resto de 2.
- q(x) es 2x+1
- r(x) es 2
En el estilo de f(x) = d(x)·q(x) + r(x), podemos escribir:
2×2−5x−1 = (x−3)(2x+1) + 2
Pero lo que necesita saber una cosa más:
El grado de r(x) es siempre menor que d(x)
Decir que dividir por un polinomio de grado 1 (tales como «x−3») el resto tendrá el grado 0 (en otras palabras, una constante, como «4»).
Usaremos esa idea en el «Teorema del Resto»:
El Teorema del resto
Cuando dividimos f (x) por el polinomio simple x-c obtenemos:
f(x) = (x−c)·q(x) + r(x)
x−c es de grado 1, por lo que r(x) debe tener el grado 0, así que solo es una constante r :
f(x) = (x−c)·q(x) + r
Ahora a ver qué pasa cuando tenemos x igual a c:
Así que tenemos esta:
El Teorema del Resto:
Cuando queremos dividir un polinomio f(x) por x−c el resto es f(c)
Así que para encontrar el resto después de dividir por x-c no necesitamos hacer ninguna división:
Simplemente calcule f (c).
Veamos que en la práctica:
Ejemplo: El resto después de 2×2-5x−1 se divide por x−3
(Nuestro ejemplo de arriba)
No necesitamos dividir por (x-3) … simplemente calcular f(3):
2(3)2-5(3)-1 = 2×9−5×3−1
= 18-15-1
= 2
Y que es el resto que recibimos de nuestros cálculos anteriores.
¡No necesitábamos hacer División Larga en absoluto!
Ejemplo: El resto después de 2×2-5x-1 se divide por x-5
El mismo ejemplo que el anterior, pero esta vez lo dividimos por «x−5»
«c» es 5, así que comprobemos f(5):
2(5)2-5(5)-1 = 2×25-5×5−1
= 50-25-1
= 24
El resto es 24
Una vez más … No necesitábamos hacer una Larga División para encontrar eso.
El Teorema del Factor
Ahora …
¿Y si calculamos f(c) y es 0?
… eso significa que el resto es 0, y …
… (x-c) debe ser un factor del polinomio!
Vemos esto al dividir números enteros. Por ejemplo, 60 ÷ 20 = 3 sin resto. Entonces 20 debe ser un factor de 60.
Ejemplo: x2−3x−4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
así que (x−4) debe ser un factor de x2−3x−4
Y así tenemos:
El Teorema de Factor:
Cuando f(c)=0, entonces x−c es un factor de f(x)
Y al revés también:
Cuando x−c es un factor de f(x) entonces f(c)=0
¿por Qué Es Útil?
Saber que x-c es un factor es lo mismo que saber que c es una raíz (y viceversa).
El factor » x-c «y la raíz» c » son lo mismo
Conocer uno y nosotros conocer el otro
Para una cosa, significa que podemos comprobar rápidamente si (x−c) es un factor del polinomio.
Ejemplo: Encuentre los factores de 2×3-x2-7x + 2
El polinomio es de grado 3, y podría ser difícil de resolver. Así que vamos a trazarlo primero:
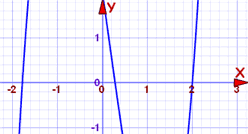
La curva cruza el eje x en tres puntos, y uno de ellos podría estar en 2. Podemos comprobar fácilmente:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Sí! f (2) = 0, así que hemos encontrado una raíz y un factor.
So (x−2) debe ser un factor de 2×3-x2-7x+2
¿Qué tal dónde cruza cerca de -1,8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
No, (x+1.8) no es un factor. Podríamos probar otros valores cercanos y quizás tener suerte.
Pero al menos sabemos que (x−2) es un factor, así que usemos la División Larga polinómica:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
Como se esperaba, el resto es cero.
Mejor aún, nos queda la ecuación cuadrática 2×2 + 3x – 1 que es fácil de resolver.
Sus raíces son -1.78… y 0,28…, por lo que el resultado final es:
2×3−x2−7x+2 = (x−2)(x+1.78…) (x-0,28…)
Pudimos resolver un polinomio difícil.
Resumen
El Teorema del Resto:
- Cuando nos dividir un polinomio f(x) por x−c el resto es f(c)
El Teorema de Factor:
- Cuando f(c)=0 entonces x−c es un factor de f(x)
- Cuando x−c es un factor de f(x) entonces f(c)=0


