eller: hvordan man undgår Polynomial lang Division, når man finder faktorer
kan du huske at gøre division i aritmetik?
“7 divideret med 2 er lig med 3 med en rest på 1”
hver del af divisionen har Navne:

som kan omskrives som et beløb som dette:
polynomer
Nå, vi kan også opdele polynomer.
F(H) L(H) = H (H) med en rest af r(H)
men det er bedre at skrive det som en sum som denne:
som i dette eksempel ved hjælp af polynomiel lang Division:
eksempel: 2H2−5h1 divideret med−3
- F (H) er 2H2-5h1
- d (H) er−3
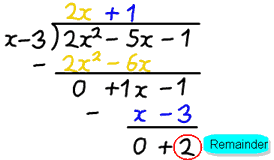
efter opdeling får vi svaret 2H+1, men der er en rest på 2.
- K(K) er 2 gange+1
- K(K) er 2
vi kan skrive:
2H2−5h−1 = (h−3) (2H+1) + 2
men du skal vide en ting mere:
graden af r (H) er altid mindre end d (H))
sig, at vi deler med et polynom af grad 1 (såsom “H−3”) resten vil have grad 0 (med andre ord en konstant, som “4”).
vi vil bruge den ide i “resten sætning”:
resten sætning
når vi deler f (h) ved det enkle polynom:
f(H) = (H−c)·K(H) + r(H)
H−C er grad 1, så r(H) skal have grad 0, så det er bare noget konstant r :
f (H) = (H−c)·K (H) + r
se nu, hvad der sker, når vi har lig med c:
så vi får dette:
resten sætning:
når vi deler et polynom f (H) med H – C resten er f (c)
så for at finde resten efter at have divideret med H-c, behøver vi ikke foretage nogen opdeling:
bare beregne f(c).
lad os se det i praksis:
eksempel: resten efter 2H2−5h−1 divideres med 3
(vores eksempel ovenfra)
vi behøver ikke at dividere med (3) … bare beregne f(3):
2(3)2-5(3)-1 = 2H9-5H3−1
= 18-15-1
= 2
og det er resten, vi fik fra vores beregninger ovenfor.
vi behøvede ikke at gøre lang Division overhovedet!
eksempel: Resten efter 2H2−5h−1 er divideret med 5
samme eksempel som ovenfor, men denne gang deler vi med “H−5”
“c” er 5, så lad os tjekke f(5):
2(5)2-5(5)-1 = 2h25-5H5−1
= 50-25-1
= 24
resten er 24
igen … Vi behøvede ikke at gøre lang Division for at finde det.
Faktorsætningen
Nu …
hvad hvis vi beregner f(c) og det er 0?
… det betyder, at resten er 0, og …
… skal være en faktor i polynomet!
vi ser dette, når vi deler hele tal. For eksempel 60 lot 20 = 3 uden resten. Så 20 skal være en faktor på 60.
eksempel: 2-3h−4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
så (4) skal være en faktor 2-3 gange−4
og så har vi:
Faktorsætningen:
når f (c)=0 så er H-C en faktor f (H)
og omvendt også:
når H-c er en faktor f (H) så f (c)=0
Hvorfor er dette nyttigt?
at vide, at C er en faktor, er det samme som at vide, at c er en rod (og omvendt).
faktoren “K−c” og roden “c” er den samme ting
Kend den ene, og vi kender den anden
for det første betyder det, at vi hurtigt kan kontrollere, om (K−c) er en faktor i polynomet.
eksempel: find faktorerne for 2H3−H2−7H+2
polynomet er grad 3 og kan være vanskeligt at løse. Så lad os plotte det først:
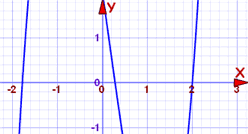
kurven krydser h-aksen på tre punkter, og en af dem kan være på 2. Vi kan kontrollere nemt:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Ja! f(2)=0, så vi har fundet en rod og en faktor.
så (H−2) skal være en faktor på 2H3-H2-7H+2
hvad med hvor det krydser nær -1.8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
1,8) er ikke en faktor. Vi kunne prøve nogle andre værdier i nærheden og måske være heldige.
men i det mindste ved vi (H−2) er en faktor, så lad os bruge polynom lang Division:
2H3−H2−7H2
3H2− 7H
3H2−6h6722>−H2 6722>−+2
0
som forventet er resten nul.
endnu bedre er vi tilbage med den kvadratiske ligning 2H2+3h−1, som er let at løse.
det er rødder er -1.78… og 0,28…, så det endelige resultat er:
2H3−H2−7H+2 = (H−2)(h+1,78…) (0, 28…)
vi var i stand til at løse et vanskeligt polynom.
Resume
resten sætning:
- når vi deler et polynom med F (C), er resten f (c)
Faktorsætningen:
- når f (c)=0 er H-c en faktor på f (H)
- når H-c er en faktor på f (H) derefter f (c)=0


