lub: jak uniknąć Wielomianowego długiego podziału przy znajdowaniu czynników
czy pamiętasz dzielenie w arytmetyce?
„7 podzielone przez 2 równa się 3 z resztą 1”
każda część podziału ma nazwy:
który można przepisać jako sumę taką:
- Wielomiany
- przykład: 2×2−5x-1 podzielone przez x−3
- twierdzeniu o pozostałej części
- przykład: reszta po 2×2-5x-1 jest dzielona przez x−3
- przykład: Reszta po 2×2−5x−1 jest dzielona przez x-5
- Twierdzenie O Czynnikach
- przykład: x2−3x−4
- dlaczego jest to przydatne?
- przykład: Znajdź czynniki 2×3−x2−7x+2
- podsumowanie
Wielomiany
cóż, możemy również podzielić wielomiany.
f(x) ÷ D(x) = q (x) z resztą R (x)
ale lepiej zapisać to jako sumę taką:
jak w tym przykładzie z wykorzystaniem wielomianu długiego podziału:
przykład: 2×2−5x-1 podzielone przez x−3
- f (x) to 2×2−5x-1
- d(x) to x−3
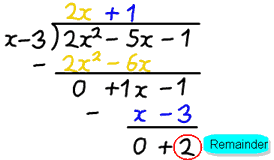
po podzieleniu otrzymujemy odpowiedź 2x+1, ale jest reszta z 2.
- q(x) to 2x+1
- r(x) to 2
w stylu f (x) = d (x) * q (x) + r (x) możemy napisać:
2×2−5x−1 = (x−3)(2x+1) + 2
ale musisz wiedzieć jeszcze jedno.:
stopień r (x) jest zawsze mniejszy niż d (x)
powiedzmy, że dzielimy przez wielomian stopnia 1 (taki jak „x−3”) reszta będzie miała stopień 0 (innymi słowy stałą, jak „4”).
użyjemy tego pomysłu w „twierdzeniu o pozostałej części”:
twierdzeniu o pozostałej części
kiedy dzielimy F(x) przez prosty wielomian x−c otrzymujemy:
f(x) = (x−c)·q (x) + r (x)
x-C jest stopniem 1, więc r (x) musi mieć stopień 0, więc jest to tylko jakaś stała r :
f(x) = (x−c)·q(x) + r
teraz zobacz, co się dzieje, gdy mamy x równe c:
więc otrzymujemy to:
twierdzenie reszty:
gdy dzielimy wielomian f (x) przez x−c, reszta to f (c)
więc aby znaleźć resztę po podzieleniu przez x-c nie musimy robić żadnego podziału:
wystarczy obliczyć f (c).
Przekonajmy się, że w praktyce:
przykład: reszta po 2×2-5x-1 jest dzielona przez x−3
(nasz przykład z góry)
nie musimy dzielić przez (x-3) … wystarczy obliczyć f(3):
2(3)2-5(3)-1 = 2×9-5×3−1
= 18-15-1
= 2
i to jest reszta, którą otrzymaliśmy z naszych obliczeń powyżej.
wcale nie musieliśmy robić długiego podziału!
przykład: Reszta po 2×2−5x−1 jest dzielona przez x-5
ten sam przykład jak powyżej, ale tym razem dzielimy przez „x−5”
„c” to 5, więc sprawdźmy f(5):
2(5)2-5(5)-1 = 2×25-5×5−1
= 50-25-1
= 24
reszta to 24
po raz kolejny … Nie musieliśmy robić długich podziałów, żeby to znaleźć.
Twierdzenie O Czynnikach
Teraz …
co jeśli obliczymy f (c)i będzie to 0?
… oznacza to, że reszta wynosi 0, i …
… (x-c) musi być czynnikiem wielomianu!
widzimy to dzieląc liczby całkowite. Na przykład 60 ÷ 20 = 3 bez reszty. Więc 20 musi być współczynnikiem 60.
przykład: x2−3x−4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
zatem (x−4) musi być czynnikiem X2-3x−4
i tak mamy:
twierdzenie o czynnikach:
gdy F(c)=0 wtedy x−c jest czynnikiem F (x)
i na odwrót:
gdy x−c jest czynnikiem F (x) wtedy f (c)=0
dlaczego jest to przydatne?
wiedząc, że X−c jest czynnikiem, to to samo, co wiedząc, że C jest pierwiastkiem (i odwrotnie).
czynnik „x−c” i pierwiastek „c” to to samo
znamy jednego i znamy drugiego
po pierwsze, oznacza to, że możemy szybko sprawdzić, czy (x−c) jest czynnikiem wielomianu.
przykład: Znajdź czynniki 2×3−x2−7x+2
wielomian ma stopień 3 i może być trudny do rozwiązania. Więc narysujmy to najpierw:
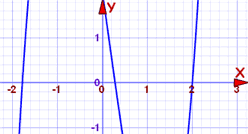
krzywa przecina oś x w trzech punktach, a jeden z nich może być w 2. Możemy łatwo sprawdzić:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
tak! f (2)=0, więc znaleźliśmy pierwiastek i czynnik.
więc (x−2) musi być współczynnikiem 2×3-x2-7x+2
co powiesz na to, gdzie krzyżuje się koło -1.8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Nie, (x+1.8) nie jest czynnikiem. Możemy spróbować innych wartości w pobliżu i może się poszczęści.
ale przynajmniej wiemy, że (x−2) jest czynnikiem, więc użyjmy wielomianu długiego dzielenia:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
zgodnie z oczekiwaniami reszta wynosi zero.
co więcej, pozostaje nam równanie kwadratowe 2×2+3x-1, które jest łatwe do rozwiązania.
to jest -1.78… i 0,28…, więc końcowy wynik to:
2×3-x2-7x+2 = (x-2) (x+1,78…) (x-0,28…
udało nam się rozwiązać trudny wielomian.
podsumowanie
twierdzenie Pozostałe:
- gdy dzielimy wielomian f (x) przez x−C, reszta to F (c)
twierdzenie o czynnikach:
- gdy f (c)=0 wtedy x-c jest czynnikiem F (x)
- gdy x−c jest czynnikiem f (x) wtedy f(C)=0



