Comment rapportez-vous une corrélation de Spearman?
La façon dont vous rapportez un coefficient de corrélation de Spearman dépend du fait que vous avez déterminé ou non la signification statistique du coefficient. Si vous avez simplement exécuté la corrélation de Spearman sans aucun test de signification statistique, vous pouvez simplement indiquer la valeur du coefficient comme indiqué ci-dessous:
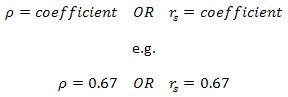
Cependant, si vous avez également exécuté des tests de signification statistique, vous devez inclure plus d’informations comme indiqué ci-dessous:
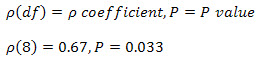
où df = N-2, où N = nombre de cas par paires.
Comment exprimez-vous l’hypothèse nulle pour ce test?
La forme générale d’une hypothèse nulle pour une corrélation de Spearman est :
H0 : Il n’y a pas d’association entre les deux variables.
N’oubliez pas que vous faites une inférence de votre échantillon à la population que l’échantillon est censé représenter. Cependant, comme il s’agit d’une compréhension générale d’un test statistique inférentiel, il n’est souvent pas inclus. Une déclaration d’hypothèse nulle pour l’exemple utilisé précédemment dans ce guide serait:
H0: Il n’y a pas d’association entre les marques mathématiques et anglaises.
Comment interpréter une corrélation de Spearman statistiquement significative ?
Il est important de réaliser que la signification statistique n’indique pas la force de la corrélation de Spearman. En fait, le test de signification statistique de la corrélation de Spearman ne vous fournit aucune information sur la force de la relation. Ainsi, atteindre une valeur de p = 0,001, par exemple, ne signifie pas que la relation est plus forte que si vous atteigniez une valeur de p = 0,04. En effet, le test de signification étudie si vous pouvez rejeter ou non l’hypothèse nulle. Si vous définissez α= 0.05, obtenir une corrélation statistiquement significative de l’ordre de rang de Spearman signifie que vous pouvez être sûr qu’il y a moins de 5% de chances que la force de la relation que vous avez trouvée (votre coefficient ρ) se soit produite par hasard si l’hypothèse nulle était vraie.