Où est une fonction à un point haut ou bas? Le calcul peut aider!
Un maximum est un point haut et un minimum est un point bas:

Dans une fonction changeant en douceur, un maximum ou un minimum est toujours là où la fonction s’aplatit (sauf pour un point de selle).
Où s’aplatit-il ? Où la pente est nulle.
Où est la pente nulle? Le dérivé nous le dit!
Plongeons avec un exemple:

- Exemple: Une balle est lancée en l’air. Sa hauteur à tout moment t est donnée par:
- Quelle est sa hauteur maximale?
- Un Rappel rapide sur les dérivées
- Comment Savons-Nous qu’il s’agit d’un Maximum (ou d’un Minimum)?
- Test de dérivée seconde
- Exemple : Trouvez les maxima et les minima pour :
- Mots
- Un autre exemple
- Exemple : Trouvez les maxima et les minima pour :
- Doit être Différentiable
- Exemple: Que diriez-vous de la fonction f(x) =/x| (valeur absolue)?
Exemple: Une balle est lancée en l’air. Sa hauteur à tout moment t est donnée par:
h = 3 + 14t−5t2
Quelle est sa hauteur maximale?
En utilisant des dérivées, nous pouvons trouver la pente de cette fonction:
![]() h = 0 + 14 − 5 (2t)
h = 0 + 14 − 5 (2t)
= 14-10t
(Voir ci-dessous cet exemple pour savoir comment nous avons trouvé cette dérivée.)

Trouvez maintenant lorsque la pente est nulle:
La pente est nulle à t = 1,4 seconde
Et la hauteur à ce moment est:
Et ainsi:
La hauteur maximale est de 12,8 m (à t = 1,4 s)
Un Rappel rapide sur les dérivées
Une dérivée trouve essentiellement la pente d’une fonction.
Dans l’exemple précédent, nous avons pris ceci:
h = 3 + 14t-5t2
et avons trouvé cette dérivée:
![]() h = 0 + 14 − 5 (2t)
h = 0 + 14 − 5 (2t)
= 14−10t
Qui nous indique la pente de la fonction à tout instant t
Nous avons utilisé ces Règles dérivées:
- La pente d’une valeur constante (comme 3) est 0
- La pente d’une droite comme 2x est 2, donc 14t a une pente de 14
- Une fonction carrée comme t2 a une pente de 2t, donc 5t2 a une pente de 5 (2t)
- Et ensuite nous les avons additionnées: 0 + 14 − 5 (2t)
Comment Savons-Nous qu’il s’agit d’un Maximum (ou d’un Minimum)?
On l’a vu sur le graphique ! Mais autrement… les produits dérivés viennent à nouveau à la rescousse.
Prenez la dérivée de la pente (la dérivée seconde de la fonction d’origine):
La dérivée de 14-10t est -10
Cela signifie que la pente devient continuellement plus petite (-10): en voyageant de gauche à droite, la pente commence positive (la fonction monte), passe par zéro (le point plat), puis la pente devient négative (la fonction tombe):

Une pente qui devient plus petite (et passe par 0) signifie un maximum.
C’est ce qu’on appelle le Test de la dérivée seconde
Sur le graphique ci-dessus, j’ai montré la pente avant et après, mais en pratique, nous faisons le test au point où la pente est nulle:
Test de dérivée seconde
Lorsque la pente d’une fonction est nulle à x et que la dérivée seconde à x est:
- inférieur à 0, c’est un maximum local
- supérieur à 0, c’est un minimum local
- égal à 0, alors le test échoue (il peut y avoir d’autres moyens de le savoir cependant)
» Dérivée seconde : moins de 0 est un maximum, plus de 0 est un minimum »
Exemple : Trouvez les maxima et les minima pour :
y = 5×3 + 2×2 -3x
La dérivée (pente) est:
![]() y = 15×2 +4x − 3
y = 15×2 +4x − 3
Qui est quadratique avec des zéros à:
- x = -3/5
- x = +1/3
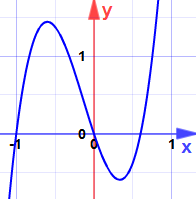
Pourraient-ils être des maxima ou des minima? (Ne regardez pas encore le graphique!)
La dérivée seconde est y »= 30x + 4
À x = -3/5:
À x = +1/3:
(Vous pouvez maintenant regarder le graphique.)
Mots
Un point haut est appelé un maximum (maxima pluriel).
Un point bas est appelé un minimum (minima au pluriel).
Le mot général pour maximum ou minimum est extremum (pluriel extrema).
Nous disons maximum local (ou minimum) lorsqu’il peut y avoir des points plus élevés (ou plus bas) ailleurs mais pas à proximité.
Un autre exemple
Exemple : Trouvez les maxima et les minima pour :
y = x3-6×2 +12x-5
La dérivée est:
![]() y = 3×2-12x + 12
y = 3×2-12x + 12
Qui est quadratique avec un seul zéro à x = 2
Est-ce un maximum ou un minimum?
La dérivée seconde est y »= 6x-12
À x = 2 :
Et voici pourquoi:
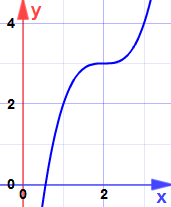
C’est un point de selle… la pente devient nulle, mais ce n’est ni un maximum ni un minimum.
Doit être Différentiable
Et il y a un point technique important:
La fonction doit être différentiable (la dérivée doit exister en chaque point de son domaine).
Exemple: Que diriez-vous de la fonction f(x) =/x| (valeur absolue)?
| | x / ressemble à ceci: |  |
À x = 0, il a un changement très pointu!
En fait, il n’y est pas différentiable (comme indiqué sur la page différentiable).
Nous ne pouvons donc pas utiliser cette méthode pour la fonction de valeur absolue.
La fonction doit également être continue, mais toute fonction différentiable est également continue, donc pas besoin de s’en soucier.
