hol van egy függvény magas vagy alacsony ponton? A kalkulus segíthet!
a maximum egy magas pont, a minimum pedig egy alacsony pont:
egy zökkenőmentesen változó függvényben a maximum vagy minimum mindig ott van, ahol a függvény ellaposodik (kivéve a nyeregpontot).
hol lapul ki? Ahol a lejtő nulla.
hol van a lejtő nulla? A származék azt mondja nekünk!
merüljünk bele egy példával:
- példa: a labdát a levegőbe dobják. Magassága bármikor t adja meg:
- mi a maximális magassága?
- a derivatívák gyors frissítése
- honnan tudjuk, hogy ez egy Maximum (vagy Minimum)?
- második derivált teszt
- példa: keresse meg a maximumokat és minimumokat:
- szavak
- még egy példa
- példa: keresse meg a maximumokat és minimumokat:
- Differenciálhatónak kell lennie
- példa: mi a helyzet az F(x) = |x| (abszolút érték) függvénnyel ?
példa: a labdát a levegőbe dobják. Magassága bármikor t adja meg:
h = 3 + 14t-5t2
mi a maximális magassága?
származékok segítségével megtalálhatjuk ennek a függvénynek a meredekségét:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
(lásd alább ezt a példát, hogyan találtuk meg ezt a származékot.)
most keresse meg, ha a meredekség nulla:
a lejtés nulla t = 1,4 másodpercnél
és a magasság akkor:
és így:
a maximális magasság 12,8 m (t = 1,4 s)
a derivatívák gyors frissítése
egy derivált alapvetően megtalálja a függvény meredekségét.
az előző példában ezt vettük:
h = 3 + 14t-5t2
és ezt a származékot találtuk ki:
![]() h = 0 + 14 − 5 (2t)
h = 0 + 14 − 5 (2t)
= 14 − 10t
amely megmondja nekünk a függvény meredekségét bármikor t
ezeket a származékos szabályokat használtuk:
- az állandó érték meredeksége (például 3) 0
- egy olyan vonal meredeksége, mint a 2x, 2, tehát a 14t meredeksége 14
- a T2-hez hasonló négyzetfüggvény meredeksége 2T, tehát az 5t2 meredeksége 5(2T)
- , majd hozzáadtuk őket: 0 + 14 − 5(2t)
honnan tudjuk, hogy ez egy Maximum (vagy Minimum)?
láttuk a grafikonon! De egyébként … a származékok ismét megmentésre kerülnek.
Vegyük a meredekség deriváltját (az eredeti függvény második deriváltja):
a 14 − 10t deriváltja -10
ez azt jelenti, hogy a meredekség folyamatosan csökken (-10): balról jobbra haladva a lejtő pozitívnak indul (a függvény emelkedik), nullán megy keresztül (a lapos pont), majd a meredekség negatívvá válik (a függvény esik):
az a meredekség, amely kisebb lesz (és 0-ra megy), maximumot jelent.
ez az úgynevezett második derivált teszt
a fenti grafikonon megmutattam a meredekséget előtte és utána, de a gyakorlatban a tesztet azon a ponton végezzük, ahol a meredekség nulla:
második derivált teszt
amikor egy függvény meredeksége nulla x-nél, a második derivált pedig x-nél:
- kevesebb, mint 0, ez egy helyi maximum
- nagyobb, mint 0, ez egy helyi minimum
- egyenlő 0, akkor a teszt sikertelen (lehet, hogy más módon kideríteni, bár)
“második derivált: 0-nál kisebb a maximum, 0-nál nagyobb a minimum”
példa: keresse meg a maximumokat és minimumokat:
y = 5×3 + 2×2-3x
a derivált (meredekség) :
![]() y = 15×2 + 4x− 3
y = 15×2 + 4x− 3
ami kvadratikus nullákkal:
- x = -3/5
- x = +1/3
lehet, hogy maximumok vagy minimumok? (Még ne nézd meg a grafikont!)
a második származék y “= 30x + 4
nál nél x = -3/5:
nál nél x = +1/3:
(most megnézheti a grafikont.)
szavak
a csúcspontot maximumnak (többes számú maximának) nevezzük.
a mélypontot minimumnak (plural minima) nevezzük.
a maximális vagy minimális általános szó extremum (többes szám extrema).
akkor mondjuk a helyi maximumot (vagy minimumot), amikor máshol lehetnek magasabb (vagy alacsonyabb) pontok, de nem a közelben.
még egy példa
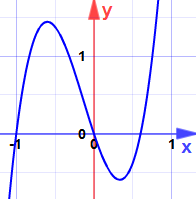
példa: keresse meg a maximumokat és minimumokat:
y = x3 − 6×2 + 12x-5
a derivált:
![]() y = 3×2 − 12x + 12
y = 3×2 − 12x + 12
melyik másodfokú, csak egy nullával x = 2
ez maximum vagy minimum?
a második származék y “= 6x − 12
At x = 2:
és itt van miért:
ez egy nyereg pont … a lejtő valóban nulla lesz, de ez sem maximális, sem minimális.
Differenciálhatónak kell lennie
és van egy fontos technikai pont:
a függvénynek differenciálhatónak kell lennie (a deriváltnak a tartományának minden pontján léteznie kell).
példa: mi a helyzet az F(x) = |x| (abszolút érték) függvénnyel ?
| |x / így néz ki: |  |
x=0-nál nagyon hegyes változás van!
valójában nem differenciálható ott (amint az a differenciálható oldalon látható).
tehát nem használhatjuk ezt a módszert az abszolút érték függvényhez.
a funkciónak is folyamatosnak kell lennie, de minden differenciálható funkció is folyamatos, ezért nem kell aggódnia.




