Dove si trova una funzione in un punto alto o basso? Il calcolo può aiutare!
Un massimo è un punto alto e un minimo è un punto basso:
In una funzione che cambia senza problemi un massimo o un minimo è sempre dove la funzione si appiattisce (ad eccezione di un punto di sella).
Dove si appiattisce? Dove la pendenza è zero.
Dov’è la pendenza zero? La Derivata ci dice!
Immergiamoci con un esempio:
- Esempio: una palla viene lanciata in aria. La sua altezza in qualsiasi momento t è data da:
- Qual è la sua altezza massima?
- Un Rapido Aggiornamento sui Derivati
- Come facciamo a sapere che è un massimo (o minimo)?
- Test della derivata seconda
- Esempio: Trovare i massimi e minimi per:
- Parole
- Un altro esempio
- Esempio: Trova i massimi e i minimi per:
- Deve essere differenziabile
- Esempio: Come circa la funzione f (x) = / x / (valore assoluto) ?
Esempio: una palla viene lanciata in aria. La sua altezza in qualsiasi momento t è data da:
h = 3 + 14t-5t2
Qual è la sua altezza massima?
Usando le derivate possiamo trovare la pendenza di quella funzione:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
(Vedi sotto questo esempio per come abbiamo trovato quella derivata.)
Ora trova quando la pendenza è zero:
La pendenza è zero in t = 1,4 secondi
E l’altezza in quel momento:
E così:
L’altezza massima è di 12,8 m (a t = 1.4 s)
Un Rapido Aggiornamento sui Derivati
Un derivato trova sostanzialmente la pendenza di una funzione.
Nell’esempio precedente abbiamo preso questo:
h = 3 + 14t-5t2
e abbiamo trovato questa derivata:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
Che ci indica la pendenza della funzione in qualsiasi tempo t
Abbiamo usato questi Derivati Regole:
- La pendenza di un valore costante (come il 3) è 0
- La pendenza di una linea come 2x è di 2, in modo da 14t ha una pendenza del 14
- Una funzione di piazza come il t2 ha una pendenza di 2t, così 5t2 ha una pendenza di 5(2t)
- E poi abbiamo aggiunto li: 0 + 14 − 5 (2 t)
Come facciamo a sapere che è un massimo (o minimo)?
L’abbiamo visto sul grafico! Ma per il resto … i derivati vengono di nuovo in soccorso.
Prendere la derivata della pendenza (la derivata seconda della funzione originale):
La Derivata di 14 − 10t è -10
Questo significa che la pendenza è continuamente sempre più piccoli (-10): in viaggio da sinistra a destra, la pendenza inizia positivo (la funzione di alzate), passa per lo zero (la punta piatta), e quindi la pendenza diventa negativa (la funzione falls):

Una pendenza che diventa più piccola (e va anche se 0) significa un massimo.
Questo è chiamato il Secondo Test derivato
Sul grafico sopra ho mostrato la pendenza prima e dopo, ma in pratica facciamo il test nel punto in cui la pendenza è zero:
Test della derivata seconda
Quando la pendenza di una funzione è zero a x e la derivata seconda a x è:
- meno di 0, è un massimo locale
- maggiore di 0, è un minimo locale
- uguale a 0, allora il test ha esito negativo (ci possono essere altri modi per capire se)
“Derivata Seconda: meno di 0 è una massima, maggiore di 0 è un minimo”
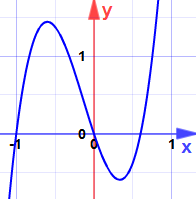
Esempio: Trovare i massimi e minimi per:
y = 5×3 + 2×2 − 3x
La derivata (pendenza) è:
![]() y = 15×2 + 4x− 3
y = 15×2 + 4x− 3
Che è di secondo grado con zeri a:
- x = -3/5
- x = +1/3
Potrebbero essere massimi o minimi? (Non guardare il grafico ancora!)
La derivata seconda y” = 30 x + 4
x = -3/5:
x = +1/3:
(Ora è possibile guardare il grafico.)
Parole
Un punto alto è chiamato massimo (massimo plurale).
Un punto basso è chiamato minimo (minimi plurali).
La parola generale per massimo o minimo è extrema (plurale extrema).
Diciamo massimo locale (o minimo) quando ci possono essere punti più alti (o più bassi) altrove ma non nelle vicinanze.
Un altro esempio
Esempio: Trova i massimi e i minimi per:
y = x3 − 6×2 + 12x-5
La derivata è:
![]() y = 3×2 − 12x + 12
y = 3×2 − 12x + 12
Che è quadratico con un solo zero a x = 2
È un massimo o un minimo?
La derivata seconda è y “= 6x – 12
At x = 2:
Ed ecco perché:
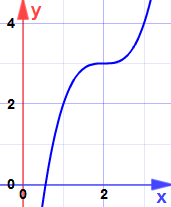
È un punto di sella … la pendenza diventa zero, ma non è né un massimo né un minimo.
Deve essere differenziabile
E c’è un importante punto tecnico:
La funzione deve essere differenziabile (la derivata deve esistere in ogni punto del suo dominio).
Esempio: Come circa la funzione f (x) = / x / (valore assoluto) ?
| |x / assomiglia a questo: |  |
A x = 0 ha un cambiamento molto appuntito!
In realtà non è differenziabile lì (come mostrato nella pagina differenziabile).
Quindi non possiamo usare questo metodo per la funzione di valore assoluto.
La funzione deve anche essere continua, ma qualsiasi funzione differenziabile è anche continua, quindi non c’è bisogno di preoccuparsi di questo.



