나머지 정리와 요인 정리

예:2 엑스 2-5 엑스-1 나누기 엑스−3

• 디(엑스)는 엑스−3

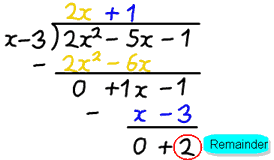
분할 후 우리는 대답 2 배+1 을 얻을 수 있지만,2 의 나머지가있다.

• 큐(엑스)는 2 배+1
• 아르 자형(엑스)이다 2

이 두 가지 유형의 방정식은 다음과 같이 쓸 수 있습니다.+1) + 2

정도 아르 자형(엑스)항상 보다 작다 디(엑스)

나머지 정리:

때 우리는 나누어 다항식 f(x) x−c 의 나머지 부분은 f(c)

이 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는 두 번째 예제에서는.. 그냥 계산 에프(3):

2(3)2-5(3)-1 = 2019-09-25−1
= 18-15-1
= 2

그리고 그것은 우리가 위의 계산에서 얻은 나머지입니다.

우리는 전혀 긴 분열을 할 필요가 없었습니다!

예:: 2338>

위와 같은 예이지만 이번에는”엑스”로 나눕니다−5″

“기음”이다 5,그래서 우리가 확인하자 에프(5):

2(5)2-5(5)-1 = 25-55-5−1
= 50-25-1
= 24

나머지는 다시 24

입니다… 우리는 그것을 찾기 위해 긴 분열을 할 필요가 없었습니다.

우리가 계산하면 에프(씨)그리고 그것은 0 입니까?

… 즉,나머지는 0 및…

… (엑스−씨)다항식의 요인이어야합니다!

예:x2−3−4

f(4) = (4)2-3(4)-4 = 16-12-4 = 0

그래서(x−4)해야 하는 요인의 x2−3−4

는 요인을 정리:

때 f(c)=0then x−c factor f(x)

과 다른 방법으로,주위에도

x−c factor f(x)그 f(c)=0

인자”엑스−씨”와 루트”씨”는 같은 것입니다

하나를 알고 우리는 다른

예:2 의 요인 찾기 엑스 3−엑스 2−7 엑스+2

다항식은 3 차이며 해결하기가 어려울 수 있습니다. 그래서 우리가 먼저 플롯 보자:

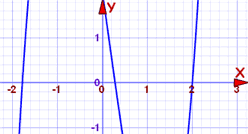
커브는 세 점에서 엑스 축을 교차하며 그 중 하나는 2 에 있을 수 있습니다. 우리는 쉽게 검사해서 좋습니다:

(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0

그래! 에프(2)=0,그래서 우리는 루트와 요인을 발견했다.이 경우 두 개의 계수를 곱해야합니다.+2

나머지 정리:

• 우리가 나눌 때 다항식 에프(엑스)에 의해 엑스−씨 나머지는 에프(씨)

요인 정리:

• 1937

1937193719371937193719371937>1937)=0