Waar is een functie op een hoog of laag punt? Calculus kan helpen!
een maximum is een hoog punt en een minimum is een laag punt:
in een soepel veranderende functie is een maximum of minimum altijd waar de functie afvlakt (met uitzondering van een zadelpunt).
Waar wordt het afgevlakt? Waar de helling nul is.
Waar is de helling nul? De afgeleide vertelt ons!
laten we er meteen in duiken met een voorbeeld:
- voorbeeld: een bal wordt in de lucht gegooid. De hoogte op enig moment t wordt gegeven door:
- Wat is de maximale hoogte?
- een snelle Refresher op derivaten
- hoe weten we dat het een Maximum (of Minimum) is?
- tweede afgeleide Test
- Voorbeeld: Het vinden van de maxima en minima voor:
- woorden
- nog een voorbeeld
- voorbeeld: Zoek de maxima en minima voor:
- moet differentieerbaar zijn
- voorbeeld: hoe zit het met de functie f (x) || x / (absolute waarde)?
voorbeeld: een bal wordt in de lucht gegooid. De hoogte op enig moment t wordt gegeven door:
h = 3 + 14t-5t2
Wat is de maximale hoogte?
met behulp van derivaten kunnen we de helling van die functie vinden:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
(zie hieronder dit voorbeeld voor hoe we die afgeleide vonden.)
vindt nu wanneer de helling nul is:
de helling is nul bij t = 1,4 seconden
en de hoogte op dat moment is:
en dus:
de maximale hoogte is 12,8 m (bij t = 1,4 s)
een snelle Refresher op derivaten
een derivaat vindt in principe de helling van een functie.
in het vorige voorbeeld namen we dit:
h = 3 + 14t-5t2
en kwamen met deze afgeleide:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
Die vertelt ons dat de helling van de functie op elk tijdstip t
We gebruikten deze Afgeleide Regels:
- De helling van een constante waarde (3) 0
- De richtingscoëfficiënt van een lijn als 2x 2, dus 14t heeft een helling van 14
- Een plein functie als t2 heeft een helling van 2t, dus 5t2 heeft een helling van 5(2t)
- En vervolgens voegden we ze: 0 + 14 − 5 (2t)
hoe weten we dat het een Maximum (of Minimum) is?
we zagen het op de grafiek! Maar verder … derivaten komen weer te hulp.
neem de afgeleide van de helling (de tweede afgeleide van de oorspronkelijke functie):
de afgeleide van 14-10t is -10
dit betekent dat de helling voortdurend kleiner wordt (-10): van links naar rechts reizen begint de helling positief (de functie stijgt), gaat door nul (het vlakke punt), en dan wordt de helling negatief (de functie valt):

een helling die kleiner wordt (en gaat door 0) betekent een maximum.
dit wordt de tweede afgeleide Test
genoemd in de grafiek hierboven I toonde de helling voor en na, maar in de praktijk doen we de test op het punt waar de helling nul is:
tweede afgeleide Test
wanneer de helling van een functie nul is bij x, en de tweede afgeleide bij x is:
- minder dan 0, het is een lokaal maximum
- groter is dan 0, wordt een lokaal minimum
- gelijk is aan 0, dan is de test mislukt (er kunnen andere manieren van het vinden van wel)
“de Tweede Afgeleide: minder dan 0 is een maximum, groter dan 0 is een minimum”
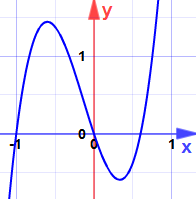
Voorbeeld: Het vinden van de maxima en minima voor:
y = 5×3 + 2×2 − 3x
De afgeleide (helling) is:
![]() y = 15×2 + 4x− 3
y = 15×2 + 4x− 3
Dat is kwadratisch met nullen op:
- x = -3/5
- x = +1/3
kunnen het maxima of minima zijn? (Kijk nog niet naar de grafiek!)
De tweede afgeleide van y” = 30x + 4
x = -3/5:
x = +1/3:
(u kunt Nu kijken naar de grafiek.)
woorden
een hoogtepunt wordt een maximum (meervoud maxima) genoemd.
een dieptepunt wordt een minimum (meervoud minima) genoemd.
het algemene woord voor maximum of minimum is extremum (meervoud extrema).
we zeggen lokaal maximum (of minimum) wanneer er hogere (of lagere) punten kunnen zijn elders, maar niet in de buurt.
nog een voorbeeld
voorbeeld: Zoek de maxima en minima voor:
y = x3-6×2 + 12x-5
het derivaat is:
![]() y = 3×2-12x + 12
y = 3×2-12x + 12
Wat is kwadratisch met slechts één nul bij x = 2
Is het een maximum of minimum?
het tweede derivaat is y “− 6x-12
bij x = 2:
en hier is waarom:
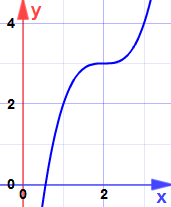
het is een zadelpunt … de helling wordt wel nul, maar het is geen maximum of minimum.
moet differentieerbaar zijn
en er is een belangrijk technisch punt:
de functie moet differentieerbaar zijn (de afgeleide moet bestaan op elk punt in zijn domein).
voorbeeld: hoe zit het met de functie f (x) || x / (absolute waarde)?
| |x / ziet er zo uit: |  |
bij x=0 heeft het een zeer puntige verandering!
in feite is het daar niet differentieerbaar (zoals getoond op de differentieerbare pagina).
dus we kunnen deze methode niet gebruiken voor de functie absolute waarde.
de functie moet ook continu zijn, maar elke functie die differentieerbaar is, is ook continu, dus maak je daar geen zorgen over.



