Logaritmer: introduktion till ”förhållandet”

återgå till lektionerna Index / gör lektionerna i ordning / Utskriftsvänlig sida

logaritmer: introduktion till
”förhållandet” (Sidan 1 av 3)

avsnitt: introduktion till loggar, förenkling av logguttryck, vanliga och naturliga loggar

logaritmer är ”motsatsen” till exponentialer, precis som subtraktion är motsatsen till addition och division är motsatsen till multiplikation. Loggar” ångra ” exponentialer. Tekniskt sett är loggar inverserna av exponentialer.

i praktiken har jag funnit det användbart att tänka på loggar när det gäller förhållandet:

på vänster sida ovan är det exponentiella uttalandet”y = bx”. På höger sida ovan är” logb(y) = x ”det ekvivalenta logaritmiska uttalandet, som uttalas” log-base-B av y är lika med x”; värdet på den prenumererade” b ”är” logaritmens bas”, precis som b är basen i det exponentiella uttrycket”bx”. Och precis som basen b i en exponentiell alltid är positiv och inte lika med 1, Så är också basen b för en logaritm alltid positiv och inte lika med 1. Vad som än är inne i logaritmen kallas loggens ”argument”. Observera att basen i både exponentiell ekvation och loggekvationen (ovan) är ”b”, men att x och y byter sida när du växlar mellan de två ekvationerna.

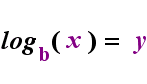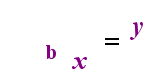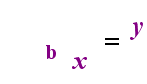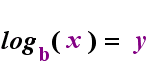
om du kan komma ihåg detta förhållande (att det som hade varit loggens argument blir ”lika” och vad som hade varit ”lika” blir exponenten i exponentiell och vice versa), då borde du inte ha för mycket problem med logaritmer.

(jag myntade termen” förhållandet ” själv. Du hittar det inte i din text, och dina lärare och handledare har ingen aning om vad du pratar om om du nämner det för dem. ”Förhållandet” är helt icke-standardterminologi. Varför använder jag det ändå? Eftersom det fungerar.)

förresten: om du märkte att jag bytte variablerna mellan de två rutorna som visar ”förhållandet”, har du ett skarpt öga. Jag gjorde det med avsikt, för att betona att poängen inte är variablerna själva, utan hur de rör sig.

• konvertera ”63 = 216” till motsvarande logaritmiska uttryck.

för att konvertera förblir basen (det vill säga 6)densamma, men 3 och 216 växlar sidor. Detta ger mig:

log6 (216) = 3 Copyright Bisexual Elizabeth Stapel 2002-2011 Alla rättigheter förbehållna

• konvertera ”log4 (1024) = 5” till motsvarande exponentiella uttryck.

för att konvertera förblir basen (det vill säga 4) densamma, men 1024 och 5 växlar sidor. Detta ger mig:

45 = 1024

topp| 1 | 2 | 3 | återgå till Index nästa >>