Pappersstorlek
Articles
0 Comments

Pappersstorlek

karta över världen som visar antagandet av ISO A4 (Blå) vs. US-brev (röd)

Huvudartikel: ISO 216
se växlingskostnader, nätverkseffekter och standardisering av möjliga skäl för olika regionala adoptionshastigheter för ISO-standardstorlekarna.

den internationella pappersstorleksstandarden är ISO 216. Den är baserad på den tyska DIN 476-standarden för pappersstorlekar. ISO-pappersstorlekar är alla baserade på ett enda bildförhållande av kvadratroten av 2, eller ungefär 1:1.41421. Det finns olika serier, liksom flera tillägg.

följande internationella pappersstorlekar ingår i Cascading Style Sheets (CSS): A3, A4, A5, B4, B5.

en serieredigera

ett storlekstabell som illustrerar ISO A-serien.

det finns 11 storlekar i A-serien, betecknad A0-A10, som alla har ett bildförhållande på A b = 2 msk 1,41421 … {\displaystyle {\frac {a}{b}} = {\sqrt {2}} \ ca 1,41421\ldots }

{\displaystyle {\frac {a}{b}}={\sqrt {2}} \ ca 1.41421 \ ldots }

, där a är långsidan och b är kortsidan.

eftersom seriestorlekarna har samma bildförhållande (2) kan de skalas till andra A – seriestorlekar utan att förvrängas, och två ark kan reduceras för att passa på exakt ett ark utan någon cutoff eller marginaler.

A0-basstorleken definieras som att den har en yta på 1 m2; med ett bildförhållande på 2, är dimensionerna för A0:

2 4 m {\displaystyle {\sqrt{2}}\, \ mathrm {m} }

{\displaystyle {\sqrt{2}}\, \ mathrm {m} }

med 1 2 4 m {\displaystyle {\frac {1} {\sqrt{2}}}\, \ mathrm {m} }

{\displaystyle {\frac {1} {\sqrt{2}}}\, \ mathrm {m} }

.

eller, avrundat till närmaste millimeter, 841 mm 1189 mm (33,1 i 46,8 tum).

en seriestorlekar är relaterade genom att den mindre dimensionen av en given storlek är den större dimensionen av nästa mindre storlek, och vikning av ett A—serieark i hälften i sin större dimension—det vill säga vikning av det i hälften parallellt med sin korta kant-resulterar i två halvor som är vardera storleken på nästa mindre a-seriestorlek. Som sådan kan en vikad broschyr av en given seriestorlek göras genom att vika ark av nästa större storlek i hälften, t.ex. A4-ark kan vikas för att göra en A5-broschyr. Det faktum att halvering av ett ark med ett bildförhållande på 2-2 resulterar i två ark som själva båda har ett bildförhållande på 2 är bevisat enligt följande:

a b = 2, {\displaystyle {\frac {a}{b}} = {\sqrt {2}},}

{\displaystyle {\frac {a}{b}} = {\sqrt {2}},}

där A är långsidan och b är kortsidan. Bildförhållandet för de nya dimensionerna på det vikta papperet är:

b a 2 = 2 b a = 2 1 2 = 2 = A b . {\displaystyle {\frac {b} {\frac {a}{2}}}=2{\frac {b}{a}} = 2{\frac {1}{\sqrt {2}}}={\sqrt {2}}={\frac {a}{b}}.}

{\displaystyle {\frac {b} {\frac {a}{2}}}=2{\frac {b}{a}} = 2{\frac {1}{\sqrt {2}}}={\sqrt {2}}={\frac {a}{b}}.}

fördelarna med att basera en pappersstorlek på ett bildförhållande på 2 2 noterades först 1786 av den tyska forskaren och filosofen Georg Christoph Lichtenberg. Formaten som blev A2, A3, B3, B4 och B5 utvecklades i Frankrike, efter att ha föreslagits av matematikern Lazare Carnot, och publicerades för rättsliga ändamål 1798, under den franska revolutionen. I början av 20-talet vände Dr Walter Porstmann Lichtenbergs ide till ett ordentligt system med olika pappersstorlekar. Porstmanns system introducerades som en DIN-standard (DIN 476) i Tyskland 1922 och ersatte en mängd andra pappersformat. Även idag kallas pappersstorlekarna ”DIN A4” (IPA:) i vardagligt bruk i Tyskland och Österrike.

DIN 476-standarden spred sig snabbt till andra länder. Före utbrottet av andra världskriget hade det antagits av följande länder:

  • Belgien (1924)
  • Nederländerna (1925)
  • Norge (1926)
  • Finland (1927)
  • Schweiz (1929)
  • Sverige (1930)
  • Sovjetunionen (1934)
  • Ungern (1938)
  • Italien (1939)

under andra världskriget antogs standarden av Uruguay (1942), Argentina (1943) och Brasilien (1943) och spred sig därefter till andra länder:

  • Spanien (1947)
  • Österrike (1948)
  • Iran (1948)
  • Rumänien (1949)
  • Japan (1951)
  • Danmark (1953)
  • Tjeckoslovakien (nu Tjeckien och Slovakien) (1953)
  • Israel (1954)
  • Portugal (1954)
  • Jugoslavien (Nu Kroatien, Serbien, Slovenien, Bosnien Och Hercegovina, Montenegro och Nordmakedonien) (1956)
  • Indien (1957)
  • Polen (1957)
  • Förenade Kungariket (1959)
  • Irland (1959)
  • Venezuela (1962)
  • Nya Zeeland (1963)
  • Island (1964)
  • Mexiko (1965)
  • Sydafrika (1966)
  • Frankrike (1967)
  • Peru (1967)
  • Turkiet (1967)
  • Chile (1968)
  • Grekland (1970)
  • Rhodesia (nu Zimbabwe) (1970)
  • Singapore (1970)
  • Bangladesh (1972)
  • Thailand (1973)
  • Barbados (1973)
  • Australien (1974)
  • Ecuador (1974)
  • Colombia (1975)
  • Kuwait (1975)
  • Kazakstan (nd.)

år 1975 använde så många länder det tyska systemet att det grundades som en ISO-standard, liksom det officiella FN-dokumentformatet. År 1977 var A4 standardbrevformatet i 88 av 148 länder. Idag har standarden antagits av alla länder i världen utom USA och Kanada. I Mexiko, Costa Rica, Colombia, Venezuela, Chile och Filippinerna är det amerikanska brevformatet fortfarande vanligt, trots deras officiella antagande av ISO-standarden.

vikten av ett A-serieark med en given pappersvikt kan beräknas genom att känna till förhållandet mellan dess storlek och A0-arket. Till exempel är ett A4-ark 1 16 16 storleken på ett A0-ark, så om det är tillverkat av 80 g/m2 papper väger det 5 g, vilket är 1 16 16 av 80 g.

b serieredigera

ett storlekstabell som illustrerar ISO B-serien.

pappersstorlekarna i b-serien är mindre vanliga än A-serien. De har samma bildförhållande i en serie:

a b = 2 = 1,41… {\displaystyle {\frac {a}{b}} = {\sqrt {2}}=1,41…}

{\displaystyle {\frac {a}{b}} = {\sqrt {2}}=1,41...}

de har dock ett annat område. Området av B-serien ark är i själva verket det geometriska medelvärdet av successiva A-serien ark. B1 är mellan A0 och A1 i storlek, med en yta på 0,707 m2 (1 msk 2 m2). Som ett resultat, B0 är 1 meter bred, och andra storlekar av serien är en halv, en fjärdedel eller ytterligare fraktioner av en meter bred: i allmänhet, varje B-storlek har en av sina sidor 1 msk effekt på två meter lång. Den sidan är kortsidan för B0, B2, B4, etc. och långsidan för B1, B3, B5, etc.

medan mindre vanligt vid kontorsbruk används B-serien för en mängd olika specialapplikationer.

  • många affischer använder papper i B-serien eller en nära approximation, såsom 50 cm 60 cm ~ B2.
  • B5 är ett relativt vanligt val för böcker.
  • B7 är lika med passstorleken ID-3 från ISO / IEC 7810.
  • B4, B5 och B6 används för kuvert som passar kuvert i C-serien.

B-serien används ofta i tryckindustrin för att beskriva både pappersstorlekar och tryckpressstorlekar, inklusive digitala pressar. B3-papper används för att skriva ut två amerikanska brev-eller A4-sidor sida vid sida med pålägg; fyra sidor skulle skrivas ut på B2, åtta på B1, etc.

C-serienRedigera

ett storlekstabell som illustrerar ISO C-serien.

C-serien definieras i ISO 269, som drogs tillbaka 2009 utan ersättning, men anges fortfarande i flera nationella standarder. Den används främst för kuvert. Området för ark i C-serien är det geometriska medelvärdet för områdena i ark i A-och B-serien med samma nummer; exempelvis är området för ett C4-ark det geometriska medelvärdet av områdena för ett A4-ark och ett B4-ark. Det betyder att C4 är något större än A4 och något mindre än B4. Den praktiska användningen av detta är att ett brev skrivet på A4-papper passar inuti ett C4-kuvert, och både A4-och C4-papper passar inuti ett B4-kuvert.

vissa kuvertformat med blandade sidor från angränsande storlekar (och därmed ett ungefärligt bildförhållande på 2:1) definieras också i nationella anpassningar av ISO-standarden, t.ex. DIN C6/C5 är 114 mm 229 mm, där den gemensamma sidan till C5 och C6 är 162 mm.

Översikt av ISO papper sizesEdit

ISO pappersstorlekar i stående vy (med rundade tums värden)
Format En rad B-serien C-serien
Storlek mm × mm tums × tums mm × mm tums × tums mm × mm tums × tum
0 841 × 1,189 33 1⁄8 × 46 19⁄24 1,000 × 1,414 39 3⁄8 × 55 2⁄3 917 × 1,297 36 1⁄12 × 51 1⁄12
1 594 × 841 23 3⁄8 × 33 1⁄8 707 × 1,000 27 5⁄6 × 39 3⁄8 648 × 917 25 1⁄2 × 36 1⁄12
2 420 × 594 16 13⁄24 × 23 3⁄8 500 × 707 19 2⁄3 × 27 5⁄6 458 × 648 18 1⁄24 × 25 1⁄2
3 297 × 420 11 17⁄24 × 16 13⁄24 353 × 500 13 11⁄12 × 19 2⁄3 324 × 458 12 3⁄4 × 18 1⁄24
4 210 × 297 8 1⁄4 × 11 17⁄24 250 × 353 9 5⁄6 × 13 11⁄12 229 × 324 9 × 12 3⁄4
5 148 × 210 5 5⁄6 × 8 1⁄4 176 × 250 6 11⁄12 × 9 5⁄6 162 × 229 6 3⁄8 × 9
6 105 × 148 4 1⁄8 × 5 5⁄6 125 × 176 4 11⁄12 × 6 11⁄12 114 × 162 4 1⁄2 × 6 3⁄8
7 74 × 105 2 11⁄12 × 4 1⁄8 88 × 125 3 11⁄24 × 4 11⁄12 81 × 114 3 5⁄24 × 4 1⁄2
8 52 × 74 2 1⁄24 × 2 11⁄12 62 × 88 2 11⁄24 × 3 11⁄24 57 × 81 2 1⁄4 × 3 5⁄24
9 37 × 52 1 11⁄24 × 2 1⁄24 44 × 62 1 3⁄4 × 2 11⁄24 40 × 57 1 7⁄12 × 2 1⁄4
10 26 × 37 1 1⁄24 × 1 11⁄24 31 × 44 1 5⁄24 × 1 3⁄4 28 × 40 1 1⁄12 × 1 7⁄12
i (1461 > (1461 > (100 r i + 1) (10 r r i+1) (10 r r i + 1) (xnumx r r i + xnumx), {\displaystyle \left (\alpha _{A}\cdot r^{i}\right)\times \left (\alpha _{A}\cdot r^{i}\right) \ times \ left (\alpha _ {A} \ cdot r ^ {i} \ right) \ times \ left (\alpha _ {A} \ cdot r ^ {i} \ right),}

{\displaystyle \left (\alpha _{A} \ cdot r^{i + 1} \ right) \ times \ left (\alpha _{A}\cdot r^{i} \ right),}

där
2 4 1000 ; r = 1 2 {\displaystyle \ alpha _{a}=({\sqrt{2}} \ cdot 1000)\, {\text{mm}}; r = {\frac {1} {\sqrt {2}}}}

{\displaystyle \ alpha _{a}=({\sqrt{2}} \ cdot 1000)\, {\text{mm}}; r = {\frac {1} {\sqrt {2}}}}
 ( 1), {\displaystyle \ left (\alpha _ {B} \ cdot r^{i + 1}\right) \times\left (\alpha _{B}\cdot r^{i} \ right) \ times \ left (\alpha _ {B} \ cdot r ^ {i} \ right),}

{\displaystyle \left (\alpha _{B} \ cdot r^{i + 1} \ right) \ times \ left (\alpha _{B}\cdot r^{i} \ right),}

där
CB B = (2 CB 1000 ) mm; r = 1 2 {\displaystyle \ alpha _{B}=({\sqrt {2}} \ cdot 1000)\, {\text{mm}};r={\frac {1} {\sqrt {2}}}}

{\displaystyle \ alpha _{B}=({\sqrt {2}} \ cdot 1000)\, {\text{mm}}; r = {\frac {1} {\sqrt {2}}}}
 ( C. C. r i + 1) C. C. C. r i + 1), {\displaystyle \ vänster (\alpha _{C} \ cdot r^{i + 1}\höger) \ gånger \ vänster (\alpha _{C}\cdot r^{i} \ höger),}

{\displaystyle \left(\alpha _{C}\cdot r^{i+1}\right)\times \left(\alpha _{C}\cdot r^{i}\right),}

där
C = ( 8 8 1000 ) mm ; R = 1 2 {\displaystyle \alpha _{C}=({\sqrt{8}}\cdot 1000)\,{\text{mm}};r={\frac {1} {\sqrt {2}}}}

{\displaystyle \ alpha _{C}=({\sqrt{8}} \ cdot 1000)\, {\text{mm}}; r = {\frac {1} {\sqrt {2}}}}

den }

\alfa

variabler är de distinkta första termerna i de tre geometriska progressionerna av samma gemensamma förhållande lika med kvadratroten av två. Var och en av de tre geometriska progressionerna (motsvarande de tre serierna A, B, C) bildas av alla möjliga pappersdimensioner (längd och bredd) i serien ordnade i minskande ordning. Detta intressanta arrangemang av dimensioner är också mycket användbart-det bildar inte bara en geometrisk progression med lätt att komma ihåg formler, det har också att varje på varandra följande par värden (som ett skjutfönster i storlek 2) automatiskt motsvarar dimensionerna för ett standardpappersformat i serien.

de toleranser som anges i standarden är

  • ±1.5 mm (0,06 tum) för dimensioner upp till 150 mm (5,9 tum),
  • ±2 mm (0,08 tum) för längder i intervallet 150 till 600 mm (5,9 till 23,6 tum) och
  • 3 mm (0,12 tum) för alla dimensioner över 600 mm (23,6 tum).

tyska originalredigera

den tyska standarden DIN 476 publicerades den 18 augusti 1922 och är den ursprungliga specifikationen för A -, B-och C-storlekarna. 1991 delades den upp i DIN 476-1 för A-och B-formaten och 476-2 för C-serien. Den förstnämnda har dragits tillbaka 2002 för att anta den internationella standarden som DIN EN ISO 216, men Del 2 har behållits och uppdaterades senast 2008.

den första och den andra upplagan av DIN 476 från 1922 och 1925 inkluderade också en D-serie.

DIN D-serie pappersstorlekar i stående vy (med rundade tumvärden)
Format D-serien
storlek mm
0 771 × 1,090 30 3⁄8 × 42 11⁄12
1 545 × 771 21 11⁄24 × 30 3⁄8
2 385 × 545 15 1⁄6 × 21 11⁄24
3 272 × 385 10 17⁄24 × 15 1⁄6
4 192 × 272 7 13⁄24 × 10 17⁄24
5 136 × 192 5 3⁄8 × 7 13⁄24
6 96 × 136 3 19⁄24 × 5 3⁄8
7 68 × 96 2 2⁄3 × 3 19⁄24
8 48 × 68 1 7⁄8 × 2 2⁄3

de minsta formaten som ursprungligen specificerades var A13 och B13, som reducerades till x10 i 1930-upplagan, liksom C8 och D8; C9 och C10 har lagts till i 1976-revisionen för kompatibilitet med fotograferingsstorlekar: C8 matchar nära 6 9 bilder, C9 och C10 matchar nära 7 7 respektive 5 5 bilder.

DIN 476:1922 små format (med rundade tumvärden)
Format a B
storlek mm 2809 > tum 2809 > mm 2809> mm 3547 > tum
11 18 × 26 17⁄24 × 1 1⁄24 22 × 31 7⁄8 × 1 5⁄24
12 13 × 18 1⁄2 × 17⁄24 15 × 22 7⁄12 × 7⁄8
13 9 × 13 3⁄8 × 1⁄2 11 × 15 5⁄12 × 7⁄12

DIN 476 ger format större än A0, betecknad med en prefixfaktor. I synnerhet listar den formaten 2A0 och 4A0, som är två gånger respektive fyra gånger storleken på A0.ISO 216: 2007 noterar dock 2A0 och 4A0 i tabellen över Huvudserier av trimmade storlekar (ISO A-serien): ”de sällan använda storlekarna som följer hör också till denna serie.”

DIN 476 överformat (med rundade tumvärden)
namn mm
4A0 1,682 × 2,378 66 5⁄24 × 93 5⁄8
2A0 1,189 × 1,682 46 19⁄24 × 66 5⁄24

DIN 476 används också för att specificera något strängare toleranser än ISO 216:

  • ±1 mm (0,04 tum) för dimensioner upp till 150 mm (5,9 tum),
  • ±1.5 mm (0,06 tum) för längder i intervallet 150 mm till 600 mm (5,9 till 23.6 tum) och
  • 2 mm (0,08 tum) för alla dimensioner över 600 mm (23,6 tum).

svenska förlängningarredigera

jämförelse av ISO 216 och svensk standard sis 014711 pappersstorlekar mellan A4 och A3 storlekar.

den svenska standarden SIS 01 47 11 generaliserade ISO-systemet med A -, B-och C-format genom att lägga till D -, E -, F-och G-format. Dess d-format sitter mellan ett B-format och nästa större a-format (precis som C sitter mellan A och nästa större B). De återstående formaten passar in mellan alla dessa format, så att sekvensen av Format A4, E4, C4, G4, B4, F4, D4, *H4, A3 är en geometrisk progression, där dimensionerna växer med en faktor 16 2 2 från en storlek till nästa. Denna sis-standard definierar emellertid inte någon storlek mellan ett D-format och nästa större a-format (kallas *H i föregående exempel).

av dessa ytterligare format är G5 (169 239 mm) och E5 (155 220 mm) populära i Sverige och Nederländerna för utskrift av avhandlingar, men de andra formaten har inte visat sig vara särskilt användbara i praktiken. De har inte antagits internationellt och den svenska standarden har dragits tillbaka.

den svenska och tyska D-serien innehåller i princip samma storlekar, men kompenseras av en, dvs DIN D4 är lika med SIS D5 och så vidare.

sis 014711 formler, inklusive det saknade steget, serie * H, mellan D och a,
n = 0 10, r = 16 2, s = √1⁄2
beteckning kortare kant längre kant
An r – 4 msk sn r + 4 msk sn
en r-3 msk sn r+5 msk sn
kn r-2 msk sn r + 6 msk sn
Gn r-1 msk sn r + 7 msk sn
Bn r 0 r + 8
Fn r + 1 msk sn r + 9 msk sn
Dn r+2 msk sn r + 10 msk sn
*Hn r+3 kg sn r + 11 kg sn
och (n-1) r + 4 msk sn R + 12 msk sn
Svenska D till G-serien
n E F G D
0 878 × 1242 958 × 1354 1044 × 1477 1091 × 1542
1 621 × 878 677 × 958 738 × 1044 771 × 1091
2 439 × 621 479 × 677 522 × 738 545 × 771
3 310 × 439 339 × 479 369 × 522 386 × 545
4 220 × 310 239 × 339 261 × 369 273 × 386
5 155 × 220 169 × 239 185 × 261 193 × 273
6 110 × 155 120 × 169 131 × 185 136 × 193
7 78 × 110 85 × 120 92 × 131 96 × 136
8 55 × 78 60 × 85 65 × 92 68 × 96
9 39 × 55 42 × 60 46 × 65 48 × 68
10 27 × 39 30 × 42 33 × 46 34 × 48

den japanska standarden JIS P 0138 definierar två huvudserier av pappersstorlekar. JIS A-serien är identisk med ISO A-serien, men med något olika toleranser. Området för B-seriepapper är 1,5 gånger det för motsvarande a-papper (i stället för faktorn 2 = 1,414… för ISO B-serien), så längdförhållandet är ungefär 1,22 gånger längden på motsvarande a-seriepapper. Bildförhållandet för papperet är detsamma som För a-seriepapper. Både A-och B-serien papper är allmänt tillgänglig i Japan, Taiwan och Kina, och de flesta kopiatorer är laddade med minst A4 och antingen en av A3, B4 och B5 papper.

Cascading Style Sheets (CSS) stöder endast de mest populära storlekarna, JIS-B4 och JIS-B5.

JIS B-serien pappersstorlekar (Plus rundade tumvärden)
storlek mm
0 1,030 × 1,456 40 13⁄24 × 57 1⁄3
1 728 × 1,030 28 2⁄3 × 40 13⁄24
2 515 × 728 20 7⁄24 × 28 2⁄3
3 364 × 515 14 1⁄3 × 20 7⁄24
4 257 × 364 10 1⁄8 × 14 1⁄3
5 182 × 257 7 1⁄6 × 10 1⁄8
6 128 × 182 5 1⁄24 × 7 1⁄6
7 91 × 128 3 7⁄12 × 5 1⁄24
8 64 × 91 2 1⁄2 × 3 7⁄12
9 45 × 64 1 19⁄24 × 2 1⁄2
10 32 × 45 1 1⁄4 × 1 19⁄24
11 22 × 32 7⁄8 × 1 1⁄4
12 16 × 22 5⁄8 × 7⁄8
JIS P 0202 raw-storlekar (plus rundade tumvärden)
storlek mm 0809 > tum 2809 > AR
A 625 × 880 24 5⁄8 × 34 5⁄8 1.408
B 765 × 1,085 30 1⁄8 × 42 17⁄24 1.418
Shiroku-ban (4-6) 788 × 1,091 31 1⁄24 × 42 23⁄24 1.385
Kiku-ban (Chrysanthenum) 636 × 939 25 1⁄24 × 36 23⁄24 1.476
900 × 1,200 35 5⁄12 × 47 1⁄4 4∶3

en populär storlek för böcker, kallad AB, kombinerar de kortare kanterna på A4 och B4. Ytterligare två med ett bildförhållande som approximerar 16: 9 är 20% smalare varianter av A6 respektive B6, de senare som härrör från skärning av B1 i 4 10-ark (sålunda ”B40”).

det finns också ett antal traditionella pappersstorlekar, som nu används mest av skrivare. De vanligaste av dessa gamla serier är Shiroku-ban och Kiku pappersstorlekar.

andra japanska pappersstorlekar (Plus rundade tumvärden)
storlek mm 0809 > tum 2809 > AR
AB 210 × 257 8 1⁄4 × 10 1⁄8 1.224
B40 103 × 182 4 1⁄24 × 7 1⁄6 1.767
35 84 × 148 3 7⁄24 × 5 5⁄6 1.762
Shiroku-ban 264 × 379 10 3⁄8 × 14 11⁄12 1.436
189 × 262 7 11⁄24 × 10 1⁄3 1.386
127 × 188 5 × 7 5⁄12 1.48
Kiku-ban 227 × 304 8 11⁄12 × 11 23⁄24 1.339
218 × 304 8 7⁄12 × 11 23⁄24 1.394
152 × 227 6 × 8 11⁄12 1.493
152 × 218 6 × 8 7⁄12 1.434

kinesiska extensionsEdit

den kinesiska standarden GB / T 148-1997, som ersatte GB 148-1989, dokumenterar standard ISO-serien, A och B, men lägger till en anpassad D-serie. Detta kinesiska format härstammar från Republiken Kina (1912-1949). D-serien är inte identisk med den svenska D-serien. Det följer inte strikt samma principer som ISO-pappersstorlekar: Bildförhållandet är bara mycket ungefär 2. Den korta sidan av en storlek är alltid 4 mm längre än den långa sidan av nästa mindre storlek. Långsidan av en storlek är alltid exakt-dvs utan ytterligare avrundning – dubbelt så lång som kortsidan av nästa mindre storlek.

SAC-pappersstorlekar (med rundade tumvärden och raw-storlekar)
Format D-serien AR Alias otrimmade storlekar
storlek mm 2809 > tum 2809 > mm 2809> mm 3547 > tum
0 764 × 1,064 30 1⁄12 × 41 7⁄8 1.3927 1K 780 × 1,080 30 17⁄24 × 42 1⁄2
1 532 × 760 20 23⁄24 × 29 11⁄12 1.4286 2K 540 × 780 21 1⁄4 × 30 17⁄24
2 380 × 528 14 23⁄24 × 20 19⁄24 1.3895 4K 390 × 540 15 3⁄8 × 21 1⁄4
3 264 × 376 10 3⁄8 × 14 19⁄24 1.4242 8K 270 × 390 10 5⁄8 × 15 3⁄8
4 188 × 260 7 5⁄12 × 10 1⁄4 1.3830 16K 195 × 270 7 2⁄3 × 10 5⁄8
5 130 × 184 5 1⁄8 × 7 1⁄4 1.4154 32K 135 × 195 5 1⁄3 × 7 2⁄3
6 92 × 126 3 5⁄8 × 4 23⁄24 1.3696 64K 97 × 135 3 5⁄6 × 5 1⁄3

den första standarden för pappersstorlek i Sovjetunionen var OST 303 år 1926. Sex år senare ersattes den av OST 5115 som i allmänhet följde DIN 476-principerna, men använde kyrilliska små bokstäver istället för latinska versaler, hade den andra raden skiftats så att 60 (B0) ungefär motsvarade B1 och, ännu viktigare, hade något olika storlekar:

OST-5115-format (1932)
Format а (A) б (B) в (V, C)
Storlek mm × mm tums × tums mm × mm tums × tums mm × mm tums × tum
0 814 × 1,152 32 1⁄24 × 45 3⁄8 747 × 1,056 29 5⁄12 × 41 7⁄12
1 576 × 814 22 2⁄3 × 32 1⁄24 528 × 747 20 19⁄24 × 29 5⁄12 628 × 888 24 17⁄24 × 34 23⁄24
2 407 × 576 16 1⁄24 × 22 2⁄3 373 × 528 14 2⁄3 × 20 19⁄24 444 × 628 17 1⁄2 × 24 17⁄24
3 288 × 407 11 1⁄3 × 16 1⁄24 264 × 373 10 3⁄8 × 14 2⁄3 314 × 444 12 3⁄8 × 17 1⁄2
4 203 × 288 8 × 11 1⁄3 186 × 264 7 1⁄3 × 10 3⁄8 222 × 314 8 3⁄4 × 12 3⁄8
5 144 × 203 5 2⁄3 × 8 132 × 186 5 5⁄24 × 7 1⁄3 157 × 222 6 1⁄6 × 8 3⁄4
6 101 × 144 3 23⁄24 × 5 2⁄3 93 × 132 3 2⁄3 × 5 5⁄24 111 × 157 4 3⁄8 × 6 1⁄6
7 72 × 101 2 5⁄6 × 3 23⁄24 66 × 93 2 7⁄12 × 3 2⁄3 78 × 111 3 1⁄12 × 4 3⁄8
8 50 × 72 1 23⁄24 × 2 5⁄6 46 × 66 1 19⁄24 × 2 7⁄12 55 × 78 2 1⁄6 × 3 1⁄12
9 36 × 50 1 5⁄12 × 1 23⁄24 33 × 46 1 7⁄24 × 1 19⁄24 39 × 55 1 13⁄24 × 2 1⁄6
10 25 × 36 1 × 1 5⁄12 23 × 33 11⁄12 × 1 7⁄24
11 18 × 25 17⁄24 × 1 16 × 23 5⁄8 × 11⁄12
12 12 × 18 11⁄24 × 17⁄24 11 × 16 5⁄12 × 5⁄8
13 9 × 12 3⁄8 × 11⁄24

den allmänna anpassningen av ISO 216 i Sovjetunionen, som ersatte OST 5115, var GOST 9327. I sin 1960-version listar den Format ner till A13, B12 och C8 och specificerar också 1 2 -, 1 4-och 1 8-prefix för att halvera den kortare sidan (upprepade gånger) för randformat, t. ex. 1 2A4 = 105 mm 297 mm.

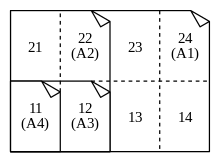
A1, A2, A3, A4 och icke-ISO storlekar som GOST 3450-60 format

en standard för tekniska ritningar från 1960, GOST 3450, introducerar alternativa numeriska formatbeteckningar för att hantera mycket höga eller mycket breda ark.Dessa 2-siffriga koder är baserade på A4 = ”11”: Den första siffran är den faktor som den längre sidan (297 mm) multipliceras med och den andra siffran är den för den kortare sidan (210 mm), så ”24” är 2 297 mm 297 mm 4 210 mm = 594 mm 840 mm.

sovjetiska format med multiplicerad kortare sida (mm)
n (×1) ×2 ×3 ×4 ×5 ×6
A0 841×1189 1682×1189 2523×1189 3364×1189 4204×1189 5045×1189
A1 594×841 = A0 1784×841 2378×841 2973×841 3568×841
A2 420×594 = A1 1261×595 1682×595 2102×595 2523×595
A3 297×420 = A2 892×420 1189×420 1487×420 1784×420
A4 210×297 = A3 631×297 841×297 1051×297 1261×297
A5 148×210 = A4 446×210 595×210 743×210 892×210
A2, A3, A4 och några av deras härledda icke-ISO-storlekar som GOST 2301-68-format

GOST 3450 från 1960 ersattes av ESKD GOST 2301 1968, men de numeriska beteckningarna förblev i populär användning mycket längre.De nya beteckningarna inte var rent numeriskt, men bestod av ISO-märkningen följas av ett ”x”, eller möjligen multiplikationstecknet ’×’, och den faktor, t ex DIN 2A0 = GOST A0×2, men DIN 4A0 ≠ GOST A0×4, som också anges är: A0×3, A1×3, A1×4, A2×3–A2×5, A3×3–A3×7, A4×3–A4×9. Format …1 och …2 vanligtvis skulle vara alias för befintliga format.

internationellt kuvert och insatsstorlekredigera

Huvudartikel: kuvert i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek i storlek

namn mm 0809 > tum 2809> AR anmärkningar 1⁄3A4 99 × 210 3 11⁄12 × 8 1⁄4 2.121 vanlig flygblad eller Rand storlek namnlösa 105 × 210 4 1⁄8 × 8 1⁄4 2∶1 standardvikt storlek på tyska bokstäver
DIN 5008 Form a

DIN 5008 (tidigare DIN 676) föreskriver bland annat två varianter, A och B, för platsen för adressfältet på första sidan i ett företagsbrev och hur man viker A4-arket i enlighet därmed, så den enda delen som är synlig för huvudinnehållet är ämnesraden.

vanliga kuvert för ISO-papper, som inte är enkla C-serien och B-serien format
namn mm 0809 > tum 2809> ar innehåll anmärkningar
DL 110 × 220 4 1⁄3 × 8 2⁄3 2∶1 1⁄3A4, DIN 5008 A och B betecknad lång, ”DIN lang” (DIN lång); ibland felaktigt kallas” DLE”, tydligen för kuvert, istället
C6 / C5 114 × 229 4 1⁄2 × 9 2∶1 vanlig kant av C6 och C5 är 161 mm;

kallas ibland ”Postfix”, ”DL+” eller ”DL Max”, men dessa termer är inte standardiserade
italienska 110 × 230 4 1⁄3 × 9 1⁄24 2.10∶1
C7 / C6 81 × 162 3 5⁄24 × 6 3⁄8 2∶1 1⁄3A5 gemensam kant av C7 och C6 är 114 mm
B6 / C4 125 × 324 4 11⁄12 × 12 3⁄4 2.6 B6 är 125 mm 176 mm, C4 är 229 mm 324 mm
Bjud in 220 × 220 8 2⁄3 × 8 2⁄3 1∶1 fyrkantigt kort med kant på A4 och A5, 210 mm
DIN E4 240 × 400 9 11⁄24 × 15 3⁄4 5∶3 anges i DIN 476-2, men inte en del av en serie korrekt

internationell råstorlekredigera

ISO 217 rå och ISO 5457 otrimmade arkstorlekar
råa mm × mm tums × tums särskilda raw mm × mm tums × tums otrimmade mm × mm tums × tums trimmas mm × mm tums × tums mm × mm tums × tum
RA0 860 × 1,220 33 3⁄4 × 48 SRA0 900 × 1,280 35 1⁄2 × 50 1⁄2 A0U 880 × 1,230 34 3⁄4 × 48 1⁄2 A0T 841 × 1,189 33 × 46 3⁄4 821 × 1,159 32 1⁄4 × 45 3⁄4
RA1 610 × 860 24 × 33 3⁄4 SRA1 640 × 900 25 1⁄4 × 35 1⁄2 A1U 625 × 880 24 1⁄2 × 34 3⁄4 A1T 594 × 841 23 1⁄2 × 33 574 × 811 22 1⁄2 × 32
RA2 430 × 610 17 × 24 SRA2 450 × 640 17 3⁄4 × 25 1⁄4 A2U 450 × 625 17 3⁄4 × 24 1⁄2 A2T 420 × 594 16 1⁄2 × 23 1⁄2 400 × 564 15 3⁄4 × 22 1⁄4
RA3 305 × 430 12 × 17 SRA3 320 × 450 12 1⁄2 × 17 3⁄4 A3U 330 × 450 13 × 17 3⁄4 A3T 297 × 420 11 3⁄4 × 16 1⁄2 277 × 390 11 × 15 1⁄4
RA4 215 × 305 8 1⁄2 × 12 SRA4 225 × 320 8 3⁄4 × 12 1⁄2 A4U 240 × 330 9 1⁄2 × 13 A4T 210 × 297 8 1⁄4 × 11 3⁄4 180 × 277 7 × 11

ISO 5457 anger ritpappersstorlekar med en trimmad storlek lika med A-seriens storlekar från A4 uppåt. De otrimmade storlekarna är 3 till 4 cm större och avrundade till närmaste centimeter. A0 till A3 används i liggande orientering, medan A4 används i stående orientering. Beteckningar för förtryckt ritpapper inkluderar basstorlekarna och ett suffix, antingen T för trimmade eller U för otrimmade ark.

den tillbakadragna standarden ISO 2784 specificerade storlekar av kontinuerliga, fläktveckade former baserade på hela tum som var vanligt för papper i kontinuerliga längder i automatisk databehandling (ADP) utrustning. Specifikt betraktades 12 tum (304,8 mm) som en otrimmad variant av A4-höjden på 297 mm.

ISO 2784:1974 korrespondens till kontinuerlig ADP papper
Storlek Acceptabla likvärdiga Direkt motsvarighet Exakta storlek Brutto storlek
tum × tums mm × mm AR tums × tums mm × mm AR mm × mm mm × mm tums × tum
A4 8 × 12 203.2 × 304.8 3∶2 8 1⁄3 × 11 2⁄3 211.7 × 296.3 7∶5 210 × 297 250 × 340 9 4⁄5 × 13 2⁄5
A5 6 × 8 152.4 × 203.2 4∶3 5 5⁄6 × 8 1⁄3 148.2 × 211.7 10∶7 148 × 210 180 × 250 7 1⁄10 × 9 4⁄5
A6 4 × 6 101.6 × 152.4 3∶2 4 1⁄6 × 5 5⁄6 105.8 × 148.2 7∶5 105 × 148 N / A N / A
A7 3 × 4 76.20 × 101.6 4∶3 N / A N / A N / A 74 × 105 N / A N / A

Lämna ett svar

Din e-postadress kommer inte publiceras.

More: