sau: cum să evitați diviziunea lungă polinomială atunci când găsiți factori
vă amintiți că ați făcut diviziunea în aritmetică?
„7 împărțit la 2 este egal cu 3 cu un rest de 1”
fiecare parte a diviziunii are nume:

care poate fi rescris ca o sumă ca aceasta:
polinoame
Ei bine, putem împărți și polinoame.
f(x) d(x) = q(x) cu un rest de r (x)
dar este mai bine să-l scrie ca o sumă ca aceasta:
ca și în acest exemplu folosind diviziune lungă polinomială:
exemplu: 2×2−5x-1 împărțit la x−3
- f (x) este 2×2-5x-1
- d (x) este x−3
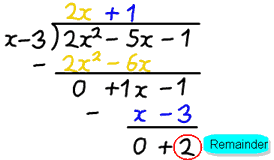
după împărțire obținem răspunsul 2x + 1, dar există un rest de 2.
- q (x) este 2x+1
- r (x) este 2
în stilul f(x) = d (x) * q (x) + r (x) putem scrie:
2×2−5x−1 = (x-3) (2x+1) + 2
dar trebuie să știți încă un lucru:
gradul de r (x) este întotdeauna mai mic decât d (x)
să spunem că împărțim la un polinom de gradul 1 (Cum ar fi „x−3”) restul va avea gradul 0 (cu alte cuvinte o constantă, cum ar fi „4”).
vom folosi această idee în”teorema restului”:
Teorema restului
când împărțim f (x) la polinomul simplu x-c obținem:
f(x) = (X−c)·q (x) + r (x)
x−c este gradul 1, deci r (x) trebuie să aibă gradul 0, deci este doar o constantă r:
f (x) = (X−c) * q(X) + r
acum vezi ce se întâmplă când avem x egal cu c:
deci, vom obține acest lucru:
Teorema restului:
când împărțim un polinom f (x) la x-c restul este f (c)
deci, pentru a găsi restul după împărțirea la x-c, nu trebuie să facem nicio diviziune:
calculați doar f(c).
să vedem că în practică:
exemplu: restul după 2×2 – 5x−1 este împărțit la x−3
(exemplul nostru de mai sus)
nu trebuie să împărțim la (x-3) … doar calcula f(3):
2(3)2-5(3)-1 = 2×9−5×3−1
= 18-15-1
= 2
și acesta este restul pe care l-am obținut din calculele noastre de mai sus.
nu am avut nevoie de a face diviziune lung, la toate!
exemplu: Restul după 2×2-5x-1 este împărțit la x-5
același exemplu ca mai sus, dar de data aceasta împărțim la „x−5”
„c” este 5, deci să verificăm f(5):
2(5)2-5(5)-1 = 2×25−5×5−1
= 50-25-1
= 24
restul este 24
încă o dată … Nu trebuia să facem o divizie lungă pentru a găsi asta.
Teorema Factorului
Acum …
ce se întâmplă dacă calculăm f (c)și este 0?
… asta înseamnă că restul este 0, și …
… (x-c) trebuie să fie un factor al polinomului!
vedem acest lucru atunci când împărțim numere întregi. De exemplu, 60 20 = 3, fără rest. Deci 20 trebuie să fie un factor de 60.
exemplu: x2−3x-4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
deci (x-4) trebuie să fie un factor de x2-3x−4
și așa avem:
Teorema factorului:
când f(c) = 0 atunci x-c este un factor de f (x)
și invers, de asemenea:
când x-c este un factor de f (x) atunci f (c)=0
de ce este util acest lucru?
a ști că x-c este un factor este același lucru cu a ști că c este o rădăcină (și invers).
factorul „X−c” și rădăcina „c” sunt același lucru
cunoașteți unul și îl cunoaștem pe celălalt
în primul rând, înseamnă că putem verifica rapid dacă (x−C) este un factor al polinomului.
exemplu: găsiți factorii 2×3−x2−7x+2
polinomul este gradul 3 și ar putea fi dificil de rezolvat. Deci, să ne complot mai întâi:
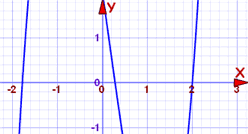
curba traversează axa x în trei puncte, iar una dintre ele ar putea fi la 2. Putem verifica cu ușurință:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Da! f (2) = 0, deci am găsit o rădăcină și un factor.
deci (x-2) trebuie să fie un factor de 2×3-x2-7x+2
ce zici de unde traversează aproape -1.8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
nu, (x+1.8) nu este un factor. Am putea încerca alte valori în apropiere și poate să avem noroc.
dar cel puțin știm (x−2) este un factor, așa că hai să folosim polinom diviziune lung:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
așa cum era de așteptat, restul este zero.
mai bine, rămânem cu ecuația pătratică 2×2+3x−1, Care este ușor de rezolvat.
rădăcinile sale sunt -1.78… și 0,28…, deci rezultatul final este:
2×3−x2−7x+2 = (x−2)(x+1,78…) (x-0,28…)
am reușit să rezolvăm un polinom dificil.
rezumat
Teorema restului:
- când împărțim un polinom f (x) la x-c restul este f (c)
Teorema factorului:
- când f(c) = 0 atunci x-c este un factor de f (x)
- când x-c este un factor de f (x) apoi f (c)=0


