Nebo: jak se vyhnout Polynomial Dlouhé Dělení při hledání faktorů,
vzpomínáš si dělení v Aritmetice?
„7 děleno 2 se rovná 3 zbytek 1“
Každá část divize má jména:
Což lze přepsat jako součet takhle:
Polynomy
No, můžeme také dělit polynomy.
f(x) ÷ d(x) = q(x) a zbytek r(x)
Ale je lepší to napsat jako součet takhle:
Jako v tomto příkladu pomocí Polynomial Dlouhé Dělení:
Příklad: 2×2−5x−1 děleno x−3
- f(x) je 2×2−5x−1
- d(x) je x−3
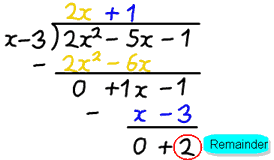
Po rozdělení dostaneme odpověď 2x+1, ale tam je zbytek 2.
- q(x), je 2x+1
- r(x) je 2
Ve stylu f(x) = d(x)·q(x) + r(x), můžeme psát:
2×2−5x−1 = (x−3)(2x+1) + 2
Ale musíte vědět jednu věc:
stupeň r(x) je vždy menší než d(x,)
Říkají, vydělíme polynom stupně 1 (jako „x−3“), zbytek bude mít stupeň 0 (jinými slovy konstantní, jako je „4“).
využijeme tuto myšlenku v „Věta o zbytcích“:
Věta o zbytcích
Při dělení f(x) jednoduchý polynom x−c, dostaneme:
f(x) = (x−c)·q(x) + r(x)
x−c je stupeň 1, takže r(x) musí být stupně 0, takže to je jen nějaká konstanta r :
f(x) = (x−c)·q(x) + r
Teď uvidíme, co se stane, když máme x se rovná c:
Takže máme tohle:
Zbytek Věty:
Při dělení polynomu f(x) x−c zbytek je f(c)
Takže najít zbytek po dělení x-c nemusíme dělat žádné rozdělení:
stačí vypočítat f(c).
podívejme se, že v praxi:
Příklad: zbytek po 2×2−5x−1 děleno x−3
(Náš příklad z výše uvedených)
nepotřebujeme se dělit (x−3) … stačí vypočítat f(3):
2(3)2-5(3)-1 = 2×9-5×3−1
= 18-15-1
= 2
a to je zbytek, který jsme získali z výše uvedených výpočtů.
nemuseli jsme dělat dlouhé dělení vůbec!
příklad: Zbytek po 2×2−5x−1 děleno x−5
Stejný příklad jako výše, ale tentokrát můžeme rozdělit podle „x−5“
„c“ je 5, takže pojďme se podívat, f(5):
2(5)2-5(5)-1 = 2×25−5×5−1
= 50-25-1
= 24
Zbytek je 24
ještě Jednou … Nepotřebovali jsme dělat dlouho divizi, abychom to našli.
Faktorová Věta
Nyní …
co když vypočítáme f (c) a je to 0?
… to znamená, že zbytek je 0, a …
… (x-c) musí být faktorem polynomu!
vidíme to při dělení celých čísel. Například 60 ÷ 20 = 3 bez zbytku. Takže 20 musí být faktor 60.
Příklad: x2−3x−4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
takže (x−4) musí být faktor x2−3x−4
A tak máme:
Faktor Věta:
Když f(c)=0, pak x−c je faktor f(x)
A naopak, příliš:
Když x−c je faktor f(x), pak f(c)=0
Proč Je To Užitečné?
vědět, že x-c je faktor, je stejné jako vědět, že c je kořen (a naopak).
faktor „x−c“ a kořen „c“ jsou stejná věc.
Víte, ten, a my víme, ostatní
Pro jednu věc, to znamená, že můžete rychle zkontrolovat, pokud (x−c) je dělitelem polynomu.
Příklad: Najít faktory, 2×3−x2−7x+2
polynom je stupně 3, a může být obtížné řešit. Pojďme to tedy nejprve vykreslit:
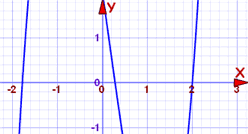
křivka protíná osu x ve třech bodech a jeden z nich může být ve 2. Můžeme snadno zkontrolovat:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Ano! f (2)=0, takže jsme našli kořen a faktor.
takže (x-2) musí být faktor 2×3-x2-7x+2
a co tam, kde se kříží blízko -1,8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Ne, (x+1.8) není faktorem. Mohli bychom zkusit nějaké jiné hodnoty poblíž a možná mít štěstí.
Ale alespoň víme, že (x−2) je faktor, takže pojďme použít Polynomial Dlouhé Dělení:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
Jak se očekávalo, zbytek je tedy nula.
ještě lepší je, že nám zbývá kvadratická rovnice 2×2+3x-1, kterou lze snadno vyřešit.
jeho kořeny jsou -1.78… a 0,28…, takže konečný výsledek je:
2×3-x2-7x+2 = (x-2) (x+1,78…) (x-0,28…)
dokázali jsme vyřešit obtížný polynom.
Shrnutí
Věta o zbytcích:
- Při dělení polynomu f(x) x−c zbytek je f(c)
Faktor Věta:
- Když je f(c)=0, pak x−c je faktor f(x)
- Když x−c je faktor f(x), pak f(c)=0



