Momento de Inercia de Área-Secciones transversales típicas I

Momento de Inercia de Área o Momento de Inercia para un Área, también conocido como Segundo Momento de Área – I, es una propiedad de forma que se utiliza para predecir la desviación, flexión y tensión en vigas.

Momento de Inercia del Área – unidades Imperiales

• inches4

Momento de Inercia del Área – unidades Métricas

• mm4
• cm4
• m4

Conversión entre Unidades de

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4.16×105 mm4 = 41.6 cm4

Ejemplo: Conversión entre Momento de Inercia de área Las unidades

9240 cm4 se pueden convertir a mm4 multiplicando por 104

(9240 cm4) 104 = 9.24 107 mm4

Momento de Inercia de Área (Momento de Inercia para un Área o un Segundo Momento de Área)

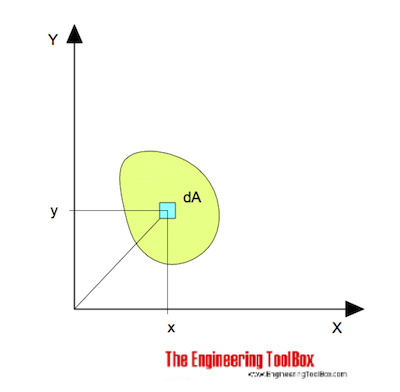
para doblar alrededor del eje x se puede expresar como

Ix = ∫ y2 dA (1)

donde

Ix = Momento de Inercia de Área relacionado con el eje x (m4, mm4, inches4)

y = la perpendicular distancia del eje x al elemento dA (m, mm, pulgadas)

dA = un área elemental (m2, mm2, pulgadas2)

El Momento de Inercia para doblar alrededor del eje y se puede expresar como

Iy = ∫ x2 dA (2)

donde

Iy = Momento de Inercia de Área relacionado con el eje y (m4, mm4, inches4)

x = la distancia perpendicular del eje y al elemento dA (m, mm, pulgadas)

Momento de Inercia de Área para la Cruz típica Secciones I

• Momento de Inercia de área para Secciones transversales típicas II

Sección Transversal Cuadrada sólida

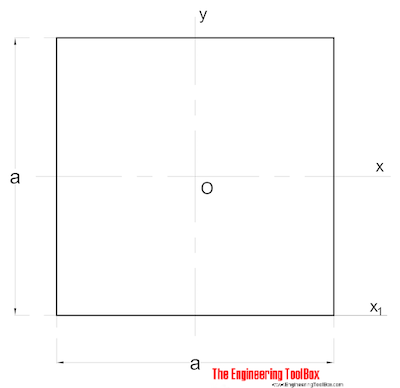
El Momento de Inercia de área para una sección cuadrada sólida se puede calcular como

Ix = a4 / 12 (2)

donde

a = lado (mm, m, pulg..)

Iy = a4 / 12 (2b)

Sección transversal rectangular sólida

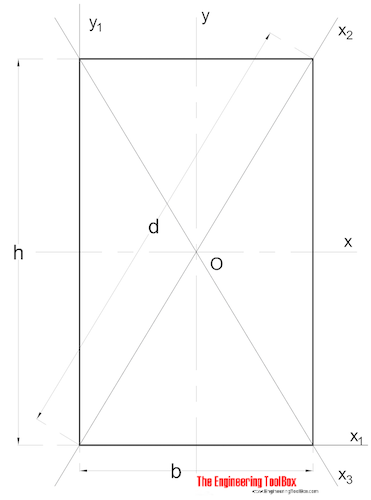
El Momento de Ineria del Área para una sección rectangular se puede calcular como

Ix = b h3 / 12 (3)

donde

b = anchura

h = altura

Iy = b3 h / 12 (3b)

Sección transversal circular sólida

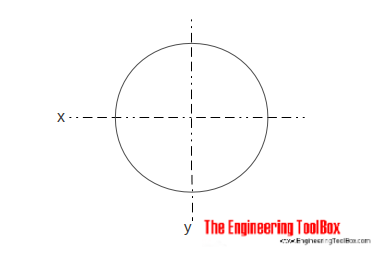
El Momento de Inercia de Área para una sección cilíndrica sólida se puede calcular como

Ix = π r4 / 4

= π d4 / 64 (4)

donde

r = radio

d = diámetro

Iy = π r4 / 4

= π d4 / 64 (4b)

Hueco Cilíndrico de Sección Transversal

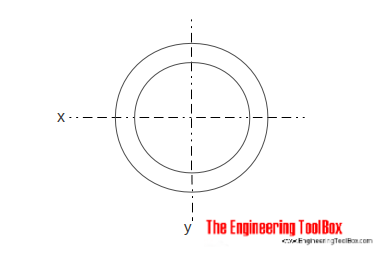
El Momento de Inercia del Área para un hueco de sección cilíndrica puede ser calculado como

Ix = π (do4 – di4) / 64 (5)

donde

do = cilindro de diámetro exterior

di = cilindro de diámetro interior

Iy = π (do4 – di4) / 64 (5b)

Sección Cuadrada – Momentos Diagonales

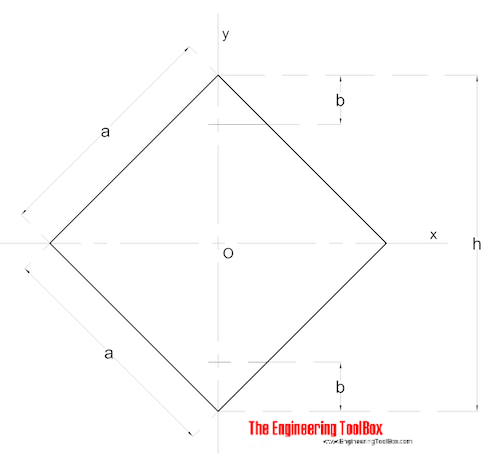
Los Momentos de Inercia de Área diagonal para una sección cuadrada se pueden calcular como

Ix = Iy = a4 / 12 (6)

Momentos de Área de Sección Rectangular en cualquier línea a través del Centro de Gravedad

La sección rectangular y el Área de Momento en línea a través del Centro de Gravedad se pueden calcular como

Ix = (b h / 12) (h2 cos2 a + b2 sin2 a) (7)

Forma simétrica

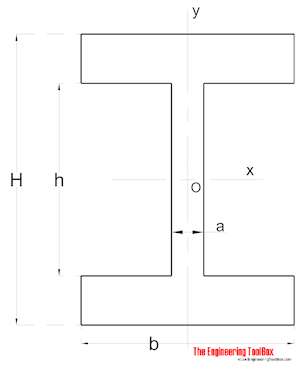
Momento de Inercia de área para a la sección de forma simétrica se puede calcular como

Ix = (a h3 / 12) + (b / 12) (H3-h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

Forma no asimétrica

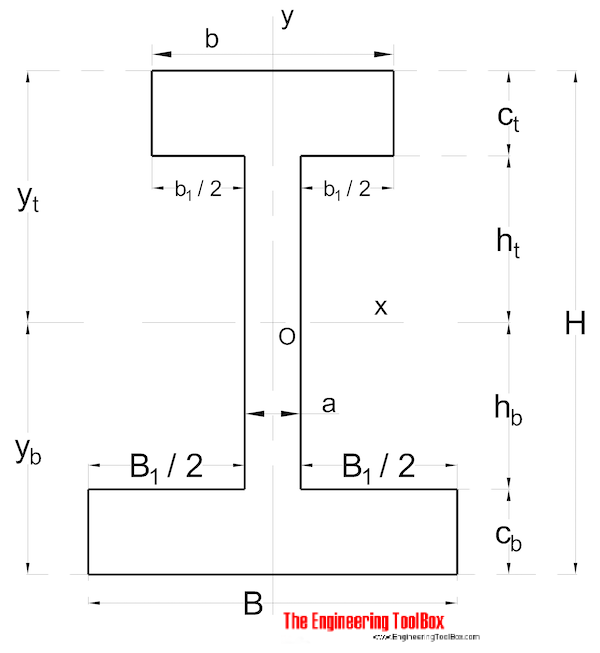
El momento de Inercia del área para una sección de forma no simétrica se puede calcular como

Ix = (1 / 3) (B yb3 – B1 hb3 + b yt3 – b1 ht3) (9)

• Momento de Inercia de área para secciones transversales típicas II

Momento de Inercia de Área vs. Momento de Inercia Polar vs. Momento de Inercia

• «Momento de Inercia de área» es una propiedad de forma que se utiliza para predecir la desviación, flexión y tensión en vigas
• «Momento de Inercia Polar» como una medida de la capacidad de un haz para resistir la torsión, que se requiere para calcular la torsión de un haz sometido a un par
• «Momento de Inercia» es una medida de la resistencia de un objeto al cambio de dirección de rotación.

Módulo de sección

• el «Módulo de sección» se define como W = I / y, donde I es el Momento de Inercia del Área y y es la distancia desde el eje neutro a cualquier fibra dada