vagy: hogyan kerüljük el a polinom hosszú osztást, amikor faktorokat találunk
emlékszel, hogy osztást végeztél aritmetikában?
“7 osztva 2-vel egyenlő 3, a fennmaradó 1”
a felosztás minden részének neve van:

amely így átírható összegként:
polinomok
nos, feloszthatjuk a polinomokat is.
f(x) d (x) = q (X) maradék r(x)
de jobb, ha ezt összegként írjuk le:
mint ebben a példában a polinom hosszú osztás használatával:
példa: 2×2−5x-1 osztva x-szel−3
- f (x) jelentése 2×2−5x-1
- d (x) jelentése x−3
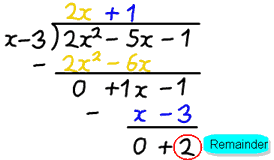
osztás után megkapjuk a választ 2x+1, de van egy maradék 2.
- q (x) jelentése 2x + 1
- r (x) jelentése 2
az F(x) = d(x)·q(x) + r(x) stílusban írhatunk:
2×2−5x−1 = (x−3)(2x+1) + 2
de még egy dolgot tudnod kell:
az r(x) foka mindig kisebb, mint d (x)
tegyük fel, hogy osztunk egy 1. fokú polinommal (például “x−3”), a maradéknak 0 foka lesz (más szóval állandó, például “4”).
ezt az ötletet a “maradék tételben” fogjuk használni:
a maradék tétel
amikor elosztjuk f(x) az egyszerű polinommal x-c kapunk:
f (x) = (x−c)·q(x) + r (x)
x-c az 1. fokozat, tehát r(x) 0. fokozattal kell rendelkeznie, tehát csak néhány állandó r :
f(x) = (x−c)·q(x) + r
most nézze meg, mi történik, ha x egyenlő c-vel:
tehát ezt kapjuk:
a maradék tétel:
amikor egy f(x) polinomot osztunk x-c-vel, a maradék F (c)
tehát ahhoz, hogy megtaláljuk a maradékot az X-c-vel való elosztás után, nem kell osztást végeznünk:
csak számítsa ki az f(c) értéket.
lássuk, hogy a gyakorlatban:
példa: a maradék után 2×2−5x−1 osztva x−3
(példánk fentről)
nem kell osztanunk (x−3) … csak kiszámítja f(3):
2(3)2-5(3)-1 = 2×9−5×3−1
= 18-15-1
= 2
és ez a maradék, amit a fenti számításokból kaptunk.
egyáltalán nem kellett hosszú osztást végeznünk!
példa: A maradék után 2×2−5x-1 osztva x-5
ugyanaz a példa, mint fent, de ezúttal osztjuk “x−5”
“c” az 5, tehát nézzük meg f(5):
2(5)2-5(5)-1 = 2×25−5×5−1
= 50-25-1
= 24
a fennmaradó rész ismét 24
… Nem kellett sokat Osztozkodnunk, hogy megtaláljuk.
A Faktor Tétel
Most …
mi van, ha f(c) – t számítunk, és ez 0?
… ez azt jelenti, hogy a maradék 0, és …
… (x-c) a polinom tényezőjének kell lennie!
ezt látjuk egész számok osztásakor. Például 60 db 20 = 3 maradék nélkül. Tehát a 20-nak 60-nak kell lennie.
példa: x2−3x−4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
tehát (x−4) x2−3x tényezőnek kell lennie−4
és így van:
a Faktortétel:
amikor f (c) = 0 akkor x-c F(x) tényezője
és fordítva is:
amikor x-c F(x) tényezője, akkor f (c)=0
miért hasznos ez?
annak ismerete, hogy x-c tényező, ugyanaz, mint annak ismerete, hogy c gyökér (és fordítva).
az “x−c” tényező és a “c” gyökér ugyanaz
ismerjük az egyiket és ismerjük a másikat
egyrészt azt jelenti, hogy gyorsan ellenőrizhetjük, hogy (x−c) a polinom tényezője.
példa: keresse meg a 2×3−x2−7x+2 tényezőit
a polinom 3 fok, és nehéz lehet megoldani. Tehát először ábrázoljuk:
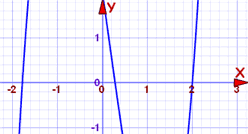
a görbe három ponton keresztezi az x tengelyt, és az egyik lehet 2. Könnyen ellenőrizhetjük:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Igen! f (2)=0, tehát találtunk egy gyökeret és egy faktort.
tehát (x-2) 2×3−x2−7x tényezőnek kell lennie+2
mit szólnál, ha keresztezi közelében -1.8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Nem, (x+1.8) nem tényező. Kipróbálhatnánk más értékeket a közelben, és talán szerencsénk lenne.
de legalább tudjuk, hogy (x−2) tényező, ezért használjuk a polinom hosszú osztását:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
ahogy az várható volt, a maradék nulla.
még jobb, ha a 2×2+3x−1 másodfokú egyenlet marad, amelyet könnyű megoldani.
gyökerei -1,78… és 0.28…, tehát a végeredmény:
2×3−x2−7x+2 = (x−2)(x+1,78…) (x−0.28…)
képesek voltunk megoldani egy nehéz polinomot.
összefoglaló
a fennmaradó tétel:
- ha egy f(x) polinomot x−c-vel osztunk, a maradék F (c)
a Faktor tétel:
- amikor f (c)=0, akkor x-c F(x) tényezője
- ha x-c F(x) tényezője, akkor f (c)=0


