円は、中心点から等距離にある同じ平面上のすべての点です。 円は境界線上の点でのみ構成されます。 円をフラフープと考えることができます。 円であるのは境界線上の点だけです。 フラフープ内の点は円の一部ではなく、内部点と呼ばれます。
中点と円の境界線との間の距離を半径と呼びます。 円の端点を持ち、中点を通過する線分を直径と呼びます。 直径は半径の2倍の大きさです。 円形の境界線上に端点があるが、中点を通過しない線分は、コードと呼ばれます。
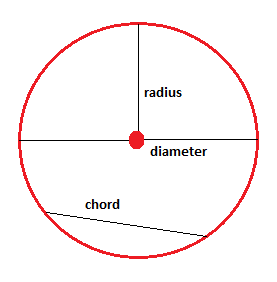
円の周りの距離は円周Cと呼ばれ、半径rまたは直径dのいずれかを使用して決定することができます:
$$\C=2\pi r$$
$$C=\pi d$ $
円は360°と同じです。 円を小さな部分に分割することができます。 円の一部は円弧と呼ばれ、その角度に応じて円弧の名前が付けられます。 円弧は、副円弧(0°<v<180°)、主円弧(180°<v<360°)、半円(v=180°)に分かれています。
円弧の長さlは、円弧の次数の尺度vと円全体の円周Cを次の式に代入することによって決定されます。
l l=c\cdot\frac{v}{v}=c\cdot\frac{v}{v}=c\cdot\frac{v}{v}=c\cdot\frac{v}{v}=c\cdot\frac{v}{v}=c\cdot\frac{v}{v}=c\cdot\frac{v}{v}$ $}{360}$$
直径が円の中心で交差するとき、それらは中心角を形成する。 あなたがケーキを切るときのように、あなたは途中であなたの作品を開始します。
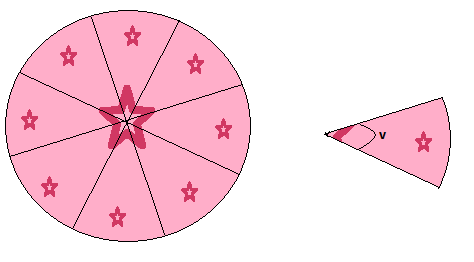
例
上記のケーキのように、円を同じ角度で8個に分割します。 円の円周は20の長さの単位です。 各ピースの円弧の長さを決定します。
まず、全円が360°であることがわかっているので、各ピースの角度が360/8=45°であることを簡単に知ることができます。 これらの値を円弧の長さの式に差し込みます。
l L=C\cdot\frac{v}{360}$$
$$l=20\cdot\frac{45}{360}=2.5$$
したがって、円弧の長さは2です。5つの長さの単位。 私たちは、同じサイズのピースの数だけ円周をダイビングするだけで、これを簡単に伝えることができました: 20/8=2.5
ビデオレッスン
シクルを同じ大きさの12個に分割した場合の円の円弧の角度は何ですか