剰余定理と因数定理

例：2×2−5x−1をxで割ったもの−3

• f(x)は2×2−5x−1
• d(x)はx−3

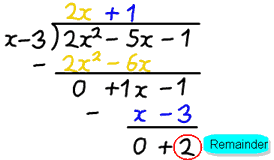
分割した後、2x+1という答えが得られますが、残りの2があります。

• q(x)は2x+1
• r(x)は2x+1である。2

f(x)=d(x)·q(x)+r(x)というスタイルでは、

2×2−5x−1=(x−3)(2x)と書くことができます+1) + 2

r(x)の次数は常にd(x)より小さい)

剰余定理：多項式f(x)をx−cで除算すると、剰余はf(c)になります)

例：2×2−5x−1の後の余りはx−3で除算されます

（上記の例）

（x−3）で除算する必要はありません。.. ちょうどfを計算します(3):

2(3)2-5(3)-1 = 2×9−5×3−1
= 18-15-1
= 2

そして、それは私たちが上記の計算から得た残りの部分です。

長い分割をする必要はまったくありませんでした！

例: 2×2−5x−1の後の余りはx−5

で除算されます上記と同じ例ですが、今回は”x”で除算します−5″

“c”は5なので、fをチェックしてみましょう(5):

2(5)2-5(5)-1 = 2×25−5×5−1
= 50-25-1
= 24

残りは再び24

です。.. それを見つけるために長い分割をする必要はありませんでした。

f(c)を計算して0とするとどうなりますか？

… これは、余りが0であることを意味し、および。..

… （x-c）は多項式の因数でなければなりません！

例：x2−3x−4

f(4) = (4)2-3(4)-4 = 16-12-4 = 0

したがって、（x−4）はx2−3xの因数でなければなりません−4

因数定理：

f（c）=0の場合、xcはf（x）

の因数であり、その逆もあります。

xcがf（x）の因数である場合、f（c）の因数である場合、xcはf（c）の因数です。)=0

因数”x−c”と根”c”は同じものです

一方を知っていて、もう一方を知っています

例：2×3−x2−7x+2の因数を求める

多項式は次数3であり、解くのが難しい可能性があります。 だから私たちは最初にそれをプロットしてみましょう:2x^3-x^2-7xのグラフ+2

曲線は3つの点でx軸と交差し、そのうちの1つが2である可能性があります。 簡単に確認できます：

f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0

はい！ f（2）=0なので、根と因子が見つかりました。

それは-1.8の近くで交差する場所はどうですか？

(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304

いいえ、（x+1.8）は因子ではありません。 私たちは近くにいくつかの他の値を試してみて、多分幸運を得ることがで 2×2+3x−1
x−2)2×3−x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
3X2−6x
-x+2
3X2-6x
-x+2
3X2-6x
-x+2
3X2-6x
-x+2
3X2-6x
-x+2
3X2-6x
-x+2
3X2-6x
-x+2
3X2-6x
-+2
0

剰余定理:

• 多項式f（x）をx−cで除算すると、余りはf（c）になります)

因子定理:

• f(c)=0のとき、x−cはf(x)
• の因数です。x−cがf(x)の因数であるとき、f(c)はf(c)の因数です)=0