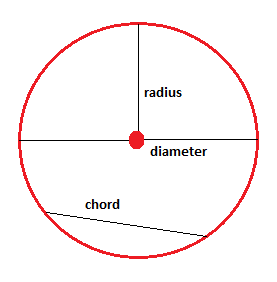
원은 중심점에서 동일한 거리에 있는 동일한 평면의 모든 점입니다. 원은 테두리의 점으로만 구성됩니다. 당신은 훌라 후프로 원을 생각할 수 있습니다. 경계의 점들만이 원입니다. 훌라 후프 내의 포인트는 원의 일부가 아니며 내부 포인트라고합니다.
중간점과 원 테두리 사이의 거리를 반지름이라고 합니다. 원에 끝점이 있고 중간점을 통과하는 선분을 지름이라고 합니다. 직경은 반경의 두 배 크기입니다. 원형 테두리에 끝점이 있지만 중간점을 통과하지 않는 선분을 코드라고합니다.
원 주위의 거리를 원주,씨,그리고 사용하여 결정할 수 있습니다 반경,아르 자형,또는 직경,디:
$$\2018-12-15$$
$$원은 360,000,000,000 원과 같습니다. 원을 더 작은 부분으로 나눌 수 있습니다. 원의 한 부분을 호라고하며 호는 각도에 따라 명명됩니다. 호으로 나누어 작은 호(0°<v<180°),주요 호(180°<v<360°)및 반원(v=180°).
호 길이,엘,아크의 정도 측정을 연결 하 여 결정 됩니다.,브이,그리고 전체 원의 둘레,씨,다음 공식에:
$$}{360}$$
직경이 원의 중심에서 교차 할 때 그들은 중앙 각도를 형성합니다. 당신이 케이크를 절단 할 때처럼 당신은 중간에 조각을 시작합니다.
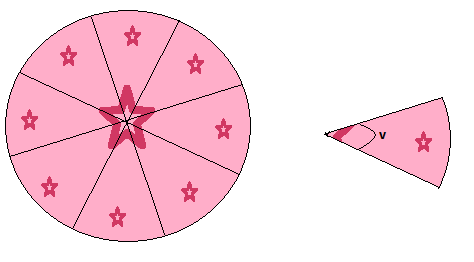
예
위의 케이크에서와 같이 우리는 원을 같은 각도로 8 조각으로 나눕니다. 원의 둘레는 20 길이 단위입니다. 각 조각의 호 길이를 결정하십시오.
먼저 우리는 완전한 원이 360 이라는 것을 알고 있기 때문에 각 조각에 대한 각도를 찾아야합니다. 이 값을 호의 길이에 대한 공식에 연결합니다.}{360}$$
$$2018-12-18 00:00:00{45}{360}=2.5$$
따라서 우리 호의 길이는 2 입니다.5 길이 단위. 우리는 단순히 같은 크기의 조각의 수에 의해 원주를 다이빙하여 더 쉽게이 말을 할 수 있었다: 20/8=2.5
비디오 레슨
우리가 12 개의 동일한 크기의 조각으로 세클을 나누면 원 호의 각도는 얼마입니까